Learning Mathematica

This notebook is Copyright © 2014 Scientific Arts, LLC,  all rights reserved.  It may be redistributed only in full and in its original form without modification; and it may not be used for any commercial purpose without permission from Scientific Arts.  A non-exclusive royalty-free license is given to reproduce and use all the of the Mathematica code in this notebook for any purpose whatsoever, as well as any of the ideas.  No guarantee whatsoever is given as to the  accuracy or functionality of anything presented in this document.  Use at your own risk. 

Enjoy! I hope that it's useful. For further information on Scientific Arts Consulting and Training, please click on the following Link:Scientific Arts.

To email, use the following address:discover@scientificarts.com.

A Mathematica notebook version of this page is located here.

Functions

In Mathematica there are many things that you can do.  Huge numbers of things.  And the things that do these are called functions.  So, I will use this word in what follows, but I will explain more of what it means a bit later on.  For now though, just assume that a function is like a machine that takes things—numbers, sets of things, pictures, sounds,...—and does things to them and then often gives you an answer.

Brackets

There are three kinds of brackets.

Parentheses: ( )

Parentheses are used to group things, just as they are used in arithmetic and algebra.  Here is an example:

Here is another example:

In the last case Mathematica does not do anything to the expression because you haven't asked it to.  But you could if you wanted to using the Mathematica function calledExpand(this uses another kind of brackets, square brackets) that we will describe in a little while):

And this is what you would expect if you did the algebra as an exercise.

Curly brackets: { }

Curly brackets are used in Mathematica to create lists of things—almost any sorts of things. You can then use these lists in many ways.

Here is an example of a list of integers:

Notice that each of the separate things (in this case the 5 integers from 1 to 5) is separated by a comma.

There are many functions in Mathematica that can create interesting lists, and there are many functions in Mathematica that do interesting things with lists.

Here is a function, calledRange,that creates a list of integers

that's the first10integers.  Notice that they are contained in curly brackets. Here are the first50integers:

Square brackets: [ ]

Functions in Mathematica generally have "arguments": they are the information that you need to give the function so that it can do what it is designed to do.  That information is given to the function within its square brackets.  So, for example the Mathematica functioPrimeQtells us whether an integer is a prime or not. You givePrimeQthat integer inside of the square brackets—this integer isPrimeQ'ssingle argument:

So, 12131993 is not a prime.

But we can factor it into its prime factors

Ok, so 12131993 is a product of a big prime and a little prime.

Some functions only allow a particular sort of information to go within the square brackets.  For example, it doesn't make sense to ask Mathematica to factor a number that is not an integer:

When Mathematica doesn't know what to do with the arguments that you give a function it just answers with what you typed.  And often it will give you a sensible error message that can help you figure out what is going on.

A function can have more than one argument, and each argument might need to be a particular type.

For example, the functionRangecan take one or two arguments, which each need to be integers

for one argument and

for two arguments.  Actually there is a three argument version as well.  Can you guess what it's doing?

Using your own symbols

Mathematica has a number of things that are symbols, that have a value.  For example the number π is represented by eitherPiorπ. And those symbols have values.  You can compute those values numerically using theNfunction:

(Even though most Mathematica functions are written out as whole words, some very common ones are written in a shorthand.  TheNfunction is one of these.)  

For more information aboutN,click here:

And you can use theNfunction with a second argument to tell Mathematica to compute the numerical value of a number to however many decimal places you want to.  Here it is where we compute the decimal value of the rational number to10 places and see that, as you expect, it is arepeating decimal.Can you see the pattern?

In Mathematica you can make your own symbols and give them values.  The way that you give a value to a symbol is using the assignment function. This is just an = sign.  But its meaning is different than it is in the mathematics that you learn in school.  Here it means that you should make a symbol "own" a value.  For example

This assigned the value9tomyValue,and Mathematica remembers this through the Mathematica session that you are in.  Here it is again:

If you want Mathematica to forget the value that you have assigned to your symbol, you can Clear it with the—you guessed it—the functionClear.

NowmyValueno longer has a value

For more information about Clear, click here:

Doing things with the symbols that you give values to

If you give a symbol a value then you can do things with it: simple things or very complex things.

Let's givexa value

Now we can do whatever we want to withx.For example, the symbol can be in an expression.  And when that expression is evaluated Mathematica will use the symbol's value to compute with it.

Notice that there is a space between the12and thexto indicate multiplication.

Here's another example:

Just for cleanliness, and so we don't make a mistake later on, let's clear the value ofx:

Often when you give a value to a symbol you don't need to see its value get printed out.  You can keep it from getting printed out by ending the Mathematica statement with a semicolon like this example.

Even though nothing printed out when you executed that,xstill has the new value

Let's get rid of that value

You do not have to have all of the things that you are doing in separate cells.  For example two or more expressions can follow one another in the same cell with each one ending in a semicolon.  Here is a simple example:

The last result without a semicolon is what is printed out.

Since I am usingxa lot I will clear it after each time I do something with it.

Here is an example that is a bit more complicated, using two symbols.  Each of the expressions is evaluated by Mathematica on after the other.  And each subsequent one uses the things that were done in the ones before it.

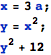
This clears bothxandy:

Making your own functions that you can reuse

Each time up to now that we have done something, we do it once.  And if we want to change it we'd need to edit it and change some of the values that are assigned.  But we'd like to be able to do what Mathematica does: to have functions of our own that take arguments in their square brackets and which we can reuse over and over by changing the values that we put in the square brackets.

We do this using "patterns" and "delayed assignments."

Patterns are, in a way, the shapes of the things we want to put into a function.  Lets make our own function that squares a number.  We will call itmySquare.

Here is one way to do it:

Thez_in this is really just a name or a tag to show that the thing that you will put in the square brackets on the left hand side should be placed in the places where azappears in the right hand side.  Then, after this is done (which is why the:=is called a delayed assignment) Mathematica evaluates the right hand side.

The way you write a pattern uses the underscore character right after the pattern's name.  The pattern is on the left hand side of the expression (the side to the left of the:=), and the name of the pattern is what it used on the right hand side (without the underscore).

When you usemySquareit does do what you expect:

And it does it with whatever you put in it

Here is a peculiar example:

If you use a variable that has a value in its argument then it will substitute that value first and then do its work

Clean things up a bit:

The cool thing is that now you can usemySquarewhenever you want to without having to write out the expression that it uses (i.e, the).

Of course squaring a number is pretty simple, but here is a more complicated example.

You wouldn't want to have to write that out each time!  But you can reuse this complicated thing over and over.

That does what you would expect, since all of the terms of the expression have anxin them except the first (the constant part of the polynomial).

Here is another example: it wouild take you a while to compute this by hand:

That's a large number....

And, for fun, here is another example where we compute the value ofmessyThingwhen its argument isπ,and we compute it to 100 decimal places.

Now let's make a new function calledpairDifferencethat takes the first item in a list of two things and subtracts it from the second item in that list.

And here is how it works:

But notice that since the way we definedpairDifferencefor Mathematica tells Mathematica only how to use a list of two things, thenpairDifferencedoesn't know how to compute something like this (with no list brackets inside it):

That's ok, since we didn't inventpairDifferenceto handle this.

Now, here's a little question.  Does the expressionpairDifference[{3,10}]have one argument or two?  

It has only one, and that argument is a list of two things.

The number of arguments of a function is the number of things that are separated by commas that are between the square brackets.  SopairDifference[{3,10}]only has one thing between its square brackets and that thing is a list.

Keeping symbols "private" (local)

One thing that  we've had to keep on doing is to Clear our symbols so that we wouldn't accidentally use one that has a value that we don't remember.  Often one makes mistakes this way when one has given a symbol a value and then forgotten that fact.  Then one uses the symbol again thinking that it doesn't have a value, or thinking that it has a different value from what it actually has.  Then surprising things can happen!

The protective box that you can put symbols into to keep them from "leaking out" with their values is called aModule. A Module has two parts: a list of the symbols that you want to keep private, and then the expressions that you want Mathematica to evaluate with those private values of the symbols.

Here is an example:

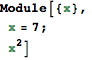
But notice that if we evaluatex"outside" of theModuleit doesn't have the value 7 that it was assigned withing theModule.

In fact it has no value because we Cleared it earlier on.

Here is another way to write the same thing that might make it clearer

I put the two statements that have to be evaluated by the Module in parentheses so you can see that they, together, are one thing: the second argument of theModule.Notice that there is no semicolon after the final statement—the , because if there was a semicolon there then nothing would get printed out at the end.  

Notice that the list of private variables (actually they are generally called "local" variables and we will use term "local' from now on) is separated from the expressions that you will execute by a comma.  Then those expressions are separated from each other with semicolons.  

Here is a funny example that gives you a hint of what is going on inside of aModulethat helps keep the local symbols "private".

Each time you evaluate that you get a result that is not x. And each time you evaluate it you get a different one. And this is how theModuleworks.  For each of the symbols in the list of local variables, Mathematica actually renames them to have a unique new name each time theModuleis executed.  You don't see this, but that is what is going one behind the scenes to make sure that the symbols do not get confused with ones that have values outside of the Module. Inside of aModuleyou can use symbols from outside theModuleas long as they are not made local by being put in theModule'slist.

Here is an example:

Notice that I wrote each seperate expression on a separate line so that I could see more clearly what is going on.

For more information aboutModule,click here:

Interlude: Some Mathematica functions that you will be using

We have already used some Mathematica functions to show some things in these notes.  Here are some of these functions along with some others for you.

Range

The Mathematica function calledRangecan be used to make easily list of integers.Rangecan be used in several different forms.

The simplest form makes a list of integers starting at 1 and going to the final integer that you tellRangeto use.  In this formRangehas one argument. Here is an example of this:

The next way you can useRangeis to give a list of the integers between two integers that you give to range.  In this formRangehas two arguments, the starting integer and the ending integer.  Here is an example of this:

The third form forRangehad three arguments: the starting integer, the ending integer, and the distance between the integers in the result.  So here is an example that gives the integers, starting at30and going to60, separated by4:

Notice that the last integer in the list is not 60.  This is because you can get to60from30by going in steps of 4.

For more information about Range, click here:

PrimeQ, and Factor Integer

PrimeQis a Mathematica function that tries to tell you whether an integer is a prime number.  For numbers that are not enormously big, it will give you an answer.PrimeQuses very advanced mathematics to do what is does. But you don't need to know how it does its work to use it.

FactorIntegerdoes exactly what you'd expect it to do: it takes an integer and gives you its prime factors.  It takes only one argument: the number that you want to factor.

PrimeQonly takes one argument, the number that you are checking to see if ti is prime. Here is an example.

Well, sincePrimeQtells us that123456789is not prime, we can useFactorIntegerto see what its prime factors are.  

For more information aboutPrimeQ,click here:

For more information about FactorInteger,click here:

Select

The Mathematica functionSelecthelps you select things from a list that have a particular property that you are interested in. Selecttakes two arguments.  The first it the list you are selecting from.  The second argument  that you giveSelectis the test you are going to give each of the elements of the list to see if it is one you want to select.

That second argument needs to be a function that givesTrueorFalse,so thatSelectknows—when the answer is True—to select an element from the list.

So here is an example. First lets make a list of integers from 100 to 200 usingRange. And let's make sure to give it a name—a symbol—and we'll call that symbolsomeIntegers.We use the = sign to assign the result of usingRangeto the symbol, and we end the statement with a semicolon so it won't print everything out, since we don't need to see those integers right now.

Now we can useSelectwithPrimeQas the test to choose the prime numbers from this list:

And those are all of the prime numbers between 100 and 200.

The sort of slightly confusing things about howPrimeQappears in the second argument ofSelectis that it doesn't have any square brackets.  But the waySelectworks is that you give it the name of the function that you want to use to test each of the elements in the list, and thenSelecttakes that function's name and wraps square brackets around each of the elements of the list and puts the function name in front of the square brackets.  Then it executes each of these and chooses the items in the list that answerTrue.

For more information aboutSelect,click here:

Partition

The Mathematica functionPartitionis another function that does helpful things to lists. It takes a list and lets you regroup the elements in the list in useful ways—and it can do this in all sorts of ways.

The first argument of thePartitionfunction is always the list that you want to do stuff to.  The other arguments of Partition tell it how to regroup the list.  There are all sorts of ways to givePartitionthese other arguments, but we'll just explore a few of them.

So, just to prepare a list for us to work with let's assign a simple list to a symbol:

I let it print out so we can use it to look at to compare things with.

Here is one way to usePartitionwith one extra argument.  This argument—which should be an integer—tellsPartitionto take the list that you give it and make it into a list of lists.

So here is an example.  In this we are tellingPartitionto break the original list into lists of5items for each, and not to let them overlap:

Here's a small but important point.  If you askPartitionto do this, but if there are not enough items in the original list to fill out the last group then Partition will just leave that last group out.

So, since 10 is not divisible by 3, thenPartitionwill leave out the last  couple of items in our original list if we ask it to break things into groups of 3 like this:

Here's one other example of usingPartitionthis way to get pairs of things out of a list:

Notice that I putRange[10]inside of thePartitionfor the first argument just for this example.  This makes sense because first Mathematica computesRange[10]and this is a list as it needs to be, and then Mathematica computes thePartitionof the result.  

This actually is generally how Mathematica works: Mathematica computes things from the inside out: it first computes the things inside of a function that it will need for that outside function to do its work.

There is one other way to usePartition(out of many others) that is very helpful for some problems.  This is to make the lists that you create withPartitionoverlap the each other.  You do this by givingPartitiona third argument that tells it how far to go before starting a new list group.

Here is an example where we make lists of length 3 that  shift by  1 from group to group (we are usingtestListagain here):

And here we make it shift by 2 each time

Can you guess what happens if we ask it to shift by 3 each time?

Well, this is what you'd expect since 3 is also the length of the group. So this is the same as the shorter way of usingPartitionwithout the third argument like the was we did it originally:

So, now that we now how to use Partition to group the items in a list in different ways, we can use it to make all of the pairs of items that are adjacent to each other like this:

For more information about Partition, click here:

Map

One more Mathematica function that is very useful for us is calledMap.

Mapis useful you have a list of things, and you have a function that you want to act on each of the things in the list individually—not on the whole list itself  but on each element of the list in turn and give back a list of the results.

Maphas two arguments—very much the way thatSelectdoes, but with them in opposite order.  The first argument is the function that you want to use on the items in the list, and the second argument is the list whose items want to use that function on.

One of the easiest ways to see whatMapcan do is to pretend that we have a function—call itemily—that Mathematica does not know about.  So whenever you use it,  Mathematica will just give you back what you wrote.  

So let's use this to see whatMapdoes.

SoMapgoes into the list and wraps square brackets around each of the items in the list and puts the function in front of each of those pairs of square brackets.

Here is an example usingPrimeQas the function and usingtestListfrom before:

So, corresponding to each of the integers from1to1 we see theTrue/Falsevalue that tells us whether that number is a prime.

Here is another example usingMapalong withemilyandPartitio to see how things work. First lets invent another symbol for pairs of numbers

So you see thatMapstill wrapsemilyaround the items in the list even though those items are in fact lists themselves.  

For more information about Map, click here:

Max and Min

Sometimes when you have a list of numbers you want to find the largest one or the smallest one—the maximum or the minimum.  The Mathematica functionsMaxandMindo this for you.

So, remembertestList?It had the numbers from1to10in it :

Obviously the maximum number here is10and the minimum one is, well,1.But at least this shows clearly howMaxandMinwork.

For more information aboutMax,click here:

For more information aboutMin,click here:

Using Modules to help create your own functions.

Now you can useModulesto make your own functions.  You will often want to do this because you will want to use local symbols to store things that you will be using later in your calculation.

Here is an example that finds the prime numbers between two integers.  It is a function with two arguments.  The Mathematica functions that it uses,Range,Select,andPrimeQ are ones that we have discussed earlier here.  But to remind yourself of what they mean you can look them up in the Mathematica Documentation Center by clicking here: or in the places earlier in this document where they are described.

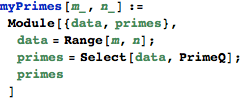
And we can now use it to find the primes between two integers without worrying whether the symbolsdataandprimeswill leak out and have values.  Their values stay within theModule.

Here are the primes between 1950 and 2010:

So you can figure out whether you were born in a prime year! 

Now here is a function that we already worked on together.  It uses all of the things we have learned so far.  Here it is, it uses the Mathematica function calledPartitionthat we talked about earlier. Also, inside of it it uses—as a local functoin inside theModule—the function calledpairDifference that we invented earlier:

And here is how it works.

Of course you have to be careful about what you put in for its arguments since this can compute a lot of primes!  Here are the results for the first primes in the first 1000 integers.  So be careful!  If you asked for the primes in the first million integers then it would take up a lot of space....

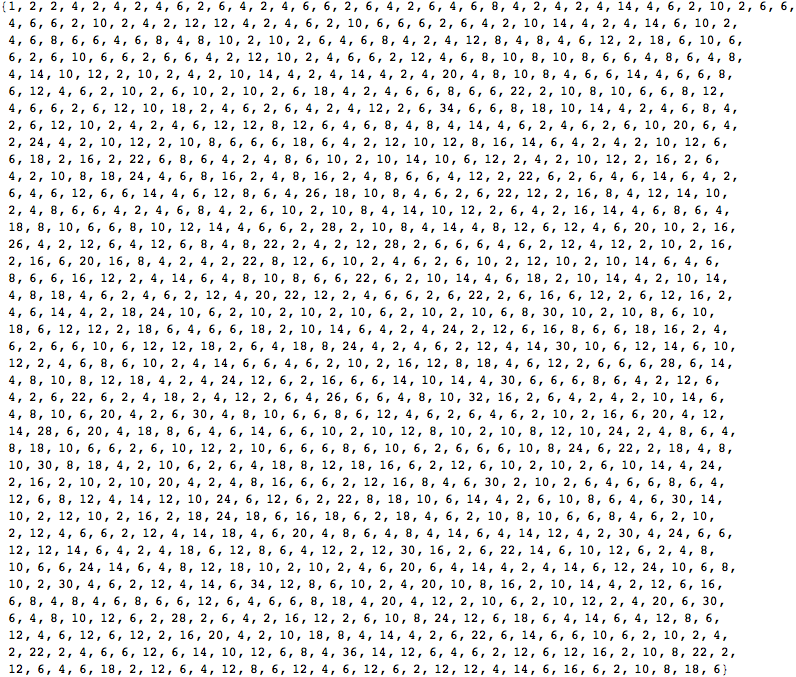
But remember that you can always assign a result to a symbol with a semicolon so that it doesn't get printed out.  Then you can use that symbol to reuse the result in a variety of other places (for example, to plot it in some way) without having to ever print it out.

So, for example, we can call this something else likeprimeDifferenceDataand end it with a semicolon so it doesn't get printed out:

Then we can ask for the biggest one amongst all of them:

Lets do this for the first 2 million numbers. But let's put both commands in the same cell so that we don't have to execute two cells.

Well, this is something that perhaps we might want to turn into a function.  So let's use what we just did here as the starting point for making that function. To do this we will need to use patterns and aModule(because we want to make the symbol primeDifferenceData a local one so it doesn't get confused with the version of it that we just used).  And we should make it a bit more general than the example above so that it can take a starting integer and an ending integer. Remember all of the commas, underscores, and semicolons that you need here. Also remember to use the := rather than a regular =.

Now we can use it

Here is an example for the the biggest prime difference that exists between and :

Pretty cool....