Motivation

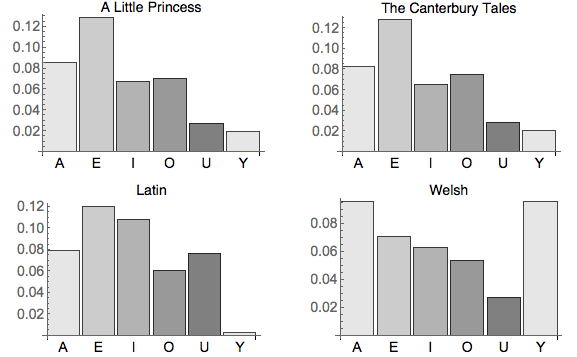
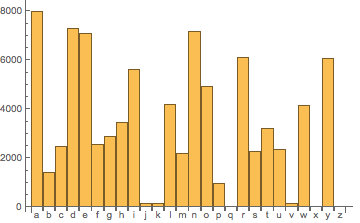
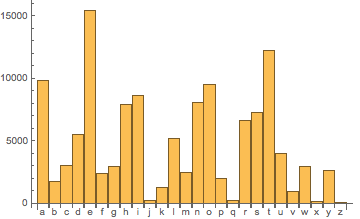
One of the things that I am most excited to offer is a hybrid method that combines Mathematica instruction in parallel with helping people develop their exxploratory and research interests.

It's a unique offering that is partially modeled on two Wolfram Research summer programs: the Mathematica Summer Camp (http://mathematica-camp.org) and the Wolfram Science summer school (https://www.wolframscience.com/summerschool). I have been an instructor at each.

In both of these the participants increase their knowledge of how to use the Mathematica computational knowledge system (or learn it from scratch) and then embark on a research project customized to their specific interests and level. The end result after a student attends either of these programs is that each person, whether they are enthusiastic pre-college or college students or seasoned, published, researchers, completes a solid project. After they leave, they often continue to evlove their projects futrher.

Though both of these take place in person during the summer, what I do is a form of one-on-one distance education. (Though if you live close to me—Arlington, Massachusetts—we may arrange to do it in person.) And I offer it to both motivated pre-college through college students as well as seasoned working scientists and engineers (including graduate students). Of course the model of how we do things together is somewhat different, appropriate to the differing needs of these two groups. And the line between them can certainly be blurry at times!

The idea in both cases is to teach how to explore fascinating aspects of the world using mathematical modeling and exploratory visualization. This is very broad and can include pretty much anything that has an aspect to it that involves quantitative calculation.

The idea is solidly grounded even though it is fundamentally wide ranging. For each person we explore the areas that they are most fascinated with—and also areas that they need to explore for additional reasons (school work, increasing progress in ongoing projects, etc,...).

Along with this we work on learning Mathematica with the goal of developing the research projects and supporting any other learning goals.

A Couple of Personal Examples

My daughter is a humanities major in college. This has been her path through her pre-college years. But she has a fine interest and ability in science and math. And, in high school, her math teachers required the students to submit proposals for the school mathematics fair.  

Year One

So in the first year I asked her what she was enthusiastic about in math. She said she loved prime numbers. So I asked her to ask a simple question about prime numbers. She thought a bit and asked if mathematicians knew how far a given prime number was from the next larger one.

“Ok, good question.  Perhaps you’d like to make exploring that your project.”

I didn’t tell her that questions like these are very deep ones that have yet to be solved by number theorists (and I didn’t point her to http://en.wikipedia.org/wiki/Prime_gap).  I said, just dive in, but first let’s learn some tools so she could explore this.

So, I taught her some of the things in Mathematica that she might need for her explorations and I guided her in creating some of the tools that she could use to play with the questions that she was curious about.  In the course of this I wrote her a tutorial about what we had learned and built together. (Here it is as a web page and here you can download it as a Mathematica notebook.)

She went on to do quite nicely in the mathematics fair, and felt proud of what she had learned and was able to do in such a short time.

Year Two

In the second year she was more focused on her interests in language, linguistics, and literature. She knew that Welsh was a odd looking language (to an English speaker) and wondered if she could tell the difference by comparing how different letters were used.

So she embarked on a project to compare different languages that use the Latin alphabet and how letter frequency—in particular vowel frequency—could be used to distinguish amongst them. Welsh really does stand out:

Just to see how one can quickly get to something like this using Mathematica, let’s import a Welsh text (http://www.gutenberg.org/cache/epub/14547/pg14547.txt) from Project Gutenberg and find out how many of each letter is in it.

Here we bring all the letter characters from this text into Mathematica as turn them all into lower case.

And here is how many of each character there is, sorted alphabetically:

Then, to see what’s going on, we make a bar graph of all the letters showing how often each appears in this particular text:

In this you can see the all important Welsh “y”!  Also “d” and “e” are quite competitive with each othe,r and “a” is the winner.

Just for fun let’s see how this compares to Alice in Wonderland in English:

Quite a different set of roles for “y”, d”,  “e”, and “a”!

After my daughter finished this portion of her project she became curious about whether she could tell the difference between different authors (in English) by analyzing the frequencies of words that they use in their works. This is an interesting problem in pattern classification. And when she did this was at about the time the Google started to provide toolsl to explore similar issues (e.g., their Ngram viewer).

It only takes a few small questions for a student to take themselves from curiosity to some of the edges of modern research. And with a powerful tool, they can begin to explore widely right away.

Lesson Learned

These two personal examples show how this process of using Mathematica to explore what one is curious about enables a student to rapidly jump in to doing things—playing around and finding their way through new places—and then, exploring whatever next tickles their curiosity.  Exploring ideas begets new questions and new ideas, and the cycle goes on and on... It's the pattern that all researchers employ.

What I do... Again

I teach the student the Mathematica system while acting as a guide and co-conspiriator in the wonderful enterprise of finding things out.

By the way, I created this web page by first writing it as a Mathematica notebook and then using the Wolfram Language to automatically turn it into a web page using the Wolfram Language function Export.