Home

Staff
     
Consulting
               
Mathematica Tools

Customer Quotes
        
Contact

Older Mathematica Items
 

 

 

 

 

Scientific Arts

RadarGeometry

•Functions and parameters contained in this package:

In[1]:=

RadarPackageFunctions[RadarGeometry, 2]

Out[1]//DisplayForm=

[Graphics:HTMLFiles/index_2.gif]

•Package functions and their basic documentation along with simple examples

•EarthEllipsoidRadius

[Graphics:HTMLFiles/index_3.gif]

Here is the earth radius (in thousands of kilometers) as a function of latitude (in degrees):

In[2]:=

Plot[EarthEllipsoidRadius[γ]/10^6, {γ, -90, 90}, Frame -> True, Axes -> False] ;

[Graphics:HTMLFiles/index_5.gif]

•ECIToECRCoordinates

[Graphics:HTMLFiles/index_6.gif]

Usage message for ECIToECRCoordinates

•ECIToTCCCoordinates

[Graphics:HTMLFiles/index_7.gif]

Usage message for ECIToTCCCoordinates

•ECRToECICoordinates

[Graphics:HTMLFiles/index_8.gif]

Usage message for ECRToECICoordinates

•ECRToGeodeticCoordinates

[Graphics:HTMLFiles/index_9.gif]

Usage message for ECRToGeodeticCoordinates

•ECRToTCCCoordinates

[Graphics:HTMLFiles/index_10.gif]

Usage message for ECRToTCCCoordinates

•ElevationAngleGeometricMaximum

[Graphics:HTMLFiles/index_11.gif]

Usage message for ElevationAngleGeometricMaximum

•ElevationAngleGeometric

[Graphics:HTMLFiles/index_12.gif]

The elevation angle is negative here because the target is close to the geometrical horizon of the transmitter-target system:

In[3]:=

N[ElevationAngleGeometric[30, 100, 55 KilometersToMeters]]

Out[3]=

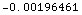
-0.0019646085228258612`

Of course closer in the elevation angle is positive

In[4]:=

N[ElevationAngleGeometric[30, 100, 10 KilometersToMeters]]

Out[4]=

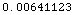
0.006411227497939014`

In[5]:=

N[ElevationAngleGeometric[30, 100, {10 KilometersToMeters}]]

Out[5]=

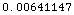
0.006411471041840211`

In[6]:=

sr = N[SlantRangeGeometric[30, 100, 10 KilometersToMeters]]

Out[6]=

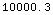
10000.320935475022`

In[7]:=

N[ElevationAngleGeometric[30, 100, {sr}]]

Out[7]=

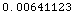
0.0064112274979689346`

•GeodeticToECRCoordinates

[Graphics:HTMLFiles/index_23.gif]

Usage message for GeodeticToECRCoordinates

•GroundRangeGeometric

[Graphics:HTMLFiles/index_24.gif]

In[8]:=

GroundRangeGeometric[30, 100, 10000.320935475022`]

Out[8]=

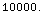
9999.999999708476`

•HorizonAngleGeometricMaximum

[Graphics:HTMLFiles/index_27.gif]

Usage message for HorizonAngleGeometricMaximum

•HorizonAngleGeometric

[Graphics:HTMLFiles/index_28.gif]

Usage message for HorizonAngleGeometric

•HorizonDirectPathDifference

[Graphics:HTMLFiles/index_29.gif]

In[9]:=

N[HorizonDirectPathDifference[30, 100, 55 KilometersToMeters]]

Out[9]=

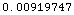
0.009197474635584513`

•HorizonDistanceCalculator

[Graphics:HTMLFiles/index_32.gif]

Usage message for HorizonDistanceCalculator

In[10]:=

HorizonDistanceCalculator[]

Out[10]=

NotebookObject[<< Horizon Distance Calculator >>]

[Graphics:HTMLFiles/index_35.gif]

•HorizonDistance

[Graphics:HTMLFiles/index_36.gif]

The distance (in Kilometers) to the geometrical horizon for a 30 meter high radar (using a 4/3 effective earth radius factior):

In[11]:=

HorizonDistance[30] MetersToKilometers // N

Out[11]=

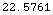
22.57607587063173`

The distance (in Kilometers) to the geometrical horizon for a 30 meter high radar (using a 4/3 effective earth radius factior) viewing a target flying at 20 meters above the ground:

In[12]:=

HorizonDistance[30, 20] MetersToKilometers // N

Out[12]=

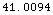
41.00937367133303`

The distance (in Kilometers) to the geometrical horizon for a 30 meter high radar (using a effective earth radius factior of unity) viewing a target flying at 10 kilometers above the ground subject to the constraint that the view must be more than 1 degree above the horizon:

In[13]:=

HorizonDistance[30, 10 KilometersToMeters, Degree, EarthRadiusScale -> 1] MetersToKilometers // N

Out[13]=

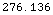
276.13574849368916`

Compare this to the case just at the geometrical horizon:

In[14]:=

HorizonDistance[30, 10 KilometersToMeters, EarthRadiusScale -> 1] MetersToKilometers // N

Out[14]=

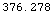
376.27785577003795`

•HorizonSpecularPathDifference

[Graphics:HTMLFiles/index_45.gif]

In[15]:=

N[HorizonSpecularPathDifference[30, 100, 55 KilometersToMeters]]

Out[15]=

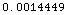
0.00144490237289574`

In[16]:=

N[HorizonSpecularPathDifference[30, 100, 55 KilometersToMeters, 1 GHz]]

Out[16]=

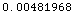
0.004819675526646304`

•LineOfSightQCalculator

[Graphics:HTMLFiles/index_50.gif]

In[17]:=

LineOfSightQCalculator[]

Out[17]=

NotebookObject[<< Line of Sight Calculator >>]

[Graphics:HTMLFiles/index_53.gif]

•LineOfSightQ

[Graphics:HTMLFiles/index_54.gif]

In[18]:=

LineOfSightQ[30, 100, 55 KilometersToMeters]

Out[18]=

True

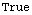
In[19]:=

HorizonDistance[30, 100.]

Out[19]=

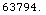
63794.02106291527`

In[20]:=

LineOfSightQ[30, 100, 55 KilometersToMeters, {1 GHz, 1}]

Out[20]=

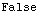
False

•RadarGeometry

[Graphics:HTMLFiles/index_61.gif]

•RAEToTCCCoordinates

[Graphics:HTMLFiles/index_62.gif]

Usage message for RAEToTCCCoordinates

•RotXInverse

[Graphics:HTMLFiles/index_63.gif]

Usage message for RotXInverse

•RotX

[Graphics:HTMLFiles/index_64.gif]

Usage message for RotX

•RotYInverse

[Graphics:HTMLFiles/index_65.gif]

Usage message for RotYInverse

•RotY

[Graphics:HTMLFiles/index_66.gif]

Usage message for RotY

•RotZInverse

[Graphics:HTMLFiles/index_67.gif]

Usage message for RotZInverse

•RotZ

[Graphics:HTMLFiles/index_68.gif]

Usage message for RotZ

•SlantRangeGeometric

[Graphics:HTMLFiles/index_69.gif]

In[21]:=

N[SlantRangeGeometric[30, 100, 23 KilometersToMeters]]

Out[21]=

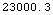
23000.27548748058`

In[22]:=

N[SlantRangeGeometric[30, 100, {0.1 Degree}]]

Out[22]=

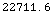
22711.60550845489`

•SpecularDirectPathDifference

[Graphics:HTMLFiles/index_74.gif]

In[23]:=

N[SpecularDirectPathDifference[30, 100, 32 KilometersToMeters]]

Out[23]=

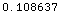
0.10863707912358223`

In[24]:=

N[SpecularDirectPathDifference[30, 100, 32 KilometersToMeters, 2 GHz]]

Out[24]=

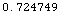
0.7247485800565552`

Here is a distance where the difference between a direct and reflected ray will be 180° out of phase, leading to destructive interference.

In[25]:=

FindRoot[SpecularDirectPathDifference[30, 100, d KilometersToMeters, 2 GHz] == 1/2, {d, {32, 33}}]

Out[25]=

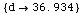
{d -> 36.933956488359954`}

•SpecularGeometryReport

[Graphics:HTMLFiles/index_81.gif]

In[26]:=

SpecularGeometryReport[30, 45, 37 KilometersToMeters]

[Graphics:HTMLFiles/index_83.gif]

•SpecularGeometry

[Graphics:HTMLFiles/index_84.gif]

In[27]:=

SpecularGeometry[30, 45, 37 KilometersToMeters] // N

Out[27]=

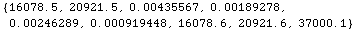
{16078.52708101374`, 20921.47291898626`, 0.004355668151733224`, 0.0018927764414473436`, 0.0024 ... 710285881`, 0.0009194483142884813`, 16078.581059835335`, 20921.571442014767`, 37000.137129813455`}

•SpecularPoint

[Graphics:HTMLFiles/index_87.gif]

In[28]:=

MetersToKilometers N[SpecularPoint[30, 65, 43 KilometersToMeters]]

Out[28]=

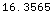
16.356532771096358`

•SunPosition

[Graphics:HTMLFiles/index_90.gif]

•TCCToECICoordinates

[Graphics:HTMLFiles/index_91.gif]

Usage message for TCCToECICoordinates

•TCCToECRCoordinates

[Graphics:HTMLFiles/index_92.gif]

Usage message for TCCToECRCoordinates

•TCCToRAECoordinates

[Graphics:HTMLFiles/index_93.gif]

Usage message for TCCToRAECoordinates

For further information on our services send email to info@scientificarts.com .
Contents of this web site Copyright © 1999-2011, Scientific Arts, LLC.

d