Home

Staff
     
Consulting
               
Mathematica Tools

Customer Quotes
        
Contact

Older Mathematica Items
 

 

 

 

 

Scientific Arts

Propagation

•Functions and parameters contained in this package:

In[1]:=

RadarPackageFunctions[Propagation, 2]

Out[1]//DisplayForm=

[Graphics:HTMLFiles/index_2.gif]

•Package functions and their basic documentation along with simple examples

•Asphalt

[Graphics:HTMLFiles/index_3.gif]

In[2]:=

ElectromagneticProperties[Asphalt, 1500 Mhz]

Out[2]=

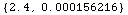
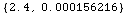
{2.4`, 0.00015621606786992803`}

{2.4`, 0.00015621606786992803`}

•Cement

[Graphics:HTMLFiles/index_7.gif]

In[3]:=

ElectromagneticProperties[Cement, 1500 Mhz]

Out[3]=

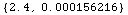
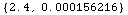
{2.4`, 0.00015621606786992803`}

{2.4`, 0.00015621606786992803`}

•ClaySoil

[Graphics:HTMLFiles/index_11.gif]

In[4]:=

ElectromagneticProperties[ClaySoil, 1500 Mhz]

Out[4]=

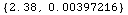
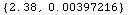
{2.38`, 0.003972160700111418`}

{2.38`, 0.003972160700111418`}

•DivergenceFactor

[Graphics:HTMLFiles/index_15.gif]

Usage message for DivergenceFactor

In[6]:=

DivergenceFactor[r _ 1, r _ 2, h _ 1, h _ 2, θ]

Out[6]=

(31855043857 (Cos[θ] Sin[θ])^(1/2) (r _ 1 + r _ 2))/(1875 2^(1/2) √ (√ ( ... θ] r _ 1 r _ 2 + r _ 2^2)) (2 r _ 1 r _ 2 + (31855043857 Sin[θ] (r _ 1 + r _ 2))/3750)))

(31855043857 (Cos[θ] Sin[θ])^(1/2) (r _ 1 + r _ 2))/(1875 2^(1/2) √ (√ ( ... θ] r _ 1 r _ 2 + r _ 2^2)) (2 r _ 1 r _ 2 + (31855043857 Sin[θ] (r _ 1 + r _ 2))/3750)))

In[7]:=

DivergenceFactor[r _ 1, r _ 2, h _ 1, h _ 2, θ, SphereRadius -> r _ e]

Out[7]=

(4 2^(1/2) (Cos[θ] Sin[θ])^(1/2) (r _ 1 + r _ 2) r _ e)/(3 √ ((2 r _ 1 r _ 2 + ... #952;] r _ 1 r _ 2 - r _ 2^2 + (64 r _ e^2)/9 + (h _ 1 + h _ 2) (h _ 1 + h _ 2 + (16 r _ e)/3)))))

(4 2^(1/2) (Cos[θ] Sin[θ])^(1/2) (r _ 1 + r _ 2) r _ e)/(3 √ ((2 r _ 1 r _ 2 + ... #952;] r _ 1 r _ 2 - r _ 2^2 + (64 r _ e^2)/9 + (h _ 1 + h _ 2) (h _ 1 + h _ 2 + (16 r _ e)/3)))))

In[8]:=

DivergenceFactor[r _ 1, r _ 2, h _ 1, h _ 2, θ, SphereRadius -> r _ e, Method -> ApproximateExpression[1]]

Out[8]=

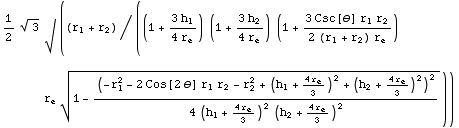
1/2 3^(1/2) √ ((r _ 1 + r _ 2)/((1 + (3 h _ 1)/(4 r _ e)) (1 + (3 h _ 2)/(4 r _ e)) (1 + ... e)/3)^2 + (h _ 2 + (4 r _ e)/3)^2)^2/(4 (h _ 1 + (4 r _ e)/3)^2 (h _ 2 + (4 r _ e)/3)^2))^(1/2)))

In[9]:=

DivergenceFactor[r _ 1, r _ 2, h _ 1, h _ 2, θ, SphereRadius -> r _ e, Method -> ApproximateExpression[2]]

Out[9]=

1/(1 + (3 Csc[θ] r _ 1 r _ 2)/(2 (r _ 1 + r _ 2) r _ e))^(1/2)

In[10]:=

DivergenceFactor[ 20, 100, 4 KilometersToMeters] // N

Out[10]=

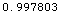
0.9978032457003813`

In[11]:=

DivergenceFactor[ 2, 2, 10 KilometersToMeters] // N

Out[11]=

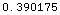
0.39017480428955575`

•EffectiveEarthRadiusFactor

[Graphics:HTMLFiles/index_30.gif]

In[12]:=

EffectiveEarthRadiusFactor[ρ]

Out[12]=

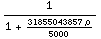
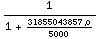
1/(1 + (31855043857 ρ)/5000)

1/(1 + (31855043857 ρ)/5000)

To determine the gradient of the index of refraction we will need to differentiate it.  Here is the index of refraction as a function of height for the 1976 US standard atmosphere

In[13]:=

ior1976 = IndexOfRefractionModelTropospheric[ Temperature1976[h], Pressure1976[h], WaterVaporDensityToPartialPressure[WaterVaporDensityMidLatitudeMean[h], Temperature1976[h]] ]

Out[13]=

1 + (0.00007759999999999999` (Pressure1976[h] + 22.193558879023307` WaterVaporDensityMidLatitudeMean[h]))/Temperature1976[h]

To differentiate this we will first need to load the Mathematica standard package NumericalMath`NLimit`

In[14]:=

Needs["NumericalMath`NLimit`"]

This package containd a function to perform numerical differentiation

In[15]:=

? ND

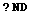
ND[expr, x, x0] gives a numerical approximation to the derivative of expr with respect to x at ... ails, ND fails. <a title=

Numerical differentiation is needed here since the expression for ior1976 does not have an explicit analytic form (Temperature1976[h], Pressure1976[h], and WaterVaporDensityMidLatitudeMean[h]).

Here is the value of the gradient of the index of refraction near sea level:

In[16]:=

ND[ior1976, h, 0]

Out[16]=

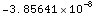
-3.856408782254526`*^-8

In[17]:=

EffectiveEarthRadiusFactor[-3.8564087571913633`*^-8]

Out[17]=

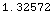
1.3257186531781366`

This value is close to the conventionally quoted 4/3 effective earth radius factor:

In[18]:=

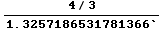
(4/3)/1.3257186531781366`

Out[18]=

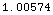
1.0057438130910674`

However, at a higher altitude the 4/3 effective earth factor is not appropriate.  For example at a height of 10 kilomenters:

In[19]:=

ND[ior1976, h, 10 KilometersToMeters]

Out[19]=

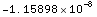
-1.158979502157293`*^-8

In[20]:=

4/3/EffectiveEarthRadiusFactor[ND[ior1976, h, 10 KilometersToMeters]]

Out[20]=

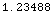
1.2348817523451077`

•ElectromagneticProperties

[Graphics:HTMLFiles/index_49.gif]

In[21]:=

SurfaceTypes[]

Out[21]=

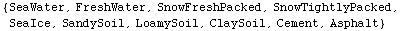
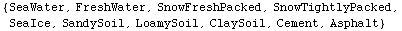
{SeaWater, FreshWater, SnowFreshPacked, SnowTightlyPacked, SeaIce, SandySoil, LoamySoil, ClaySoil, Cement, Asphalt}

{SeaWater, FreshWater, SnowFreshPacked, SnowTightlyPacked, SeaIce, SandySoil, LoamySoil, ClaySoil, Cement, Asphalt}

In[22]:=

ElectromagneticProperties[LoamySoil, 2 Ghz]

Out[22]=

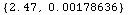
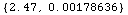
{2.47`, 0.0017863596649940845`}

{2.47`, 0.0017863596649940845`}

•FreeSpace

[Graphics:HTMLFiles/index_56.gif]

In[23]:=

PropagationFactorOneWay[FreeSpace[r, ν]]

Out[23]=

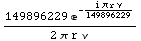
(149896229 e^(-(i π r ν)/149896229))/(2 π r ν)

In[24]:=

PropagationFactorOneWay[FreeSpace[r, Frequency[λ]]]

Out[24]=

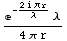
(e^(-(2 i π r)/λ) λ)/(4 π r)

In[25]:=

PropagationFactorTwoWay[FreeSpace[r, ν]]

Out[25]=

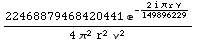
(22468879468420441 e^(-(2 i π r ν)/149896229))/(4 π^2 r^2 ν^2)

In[26]:=

PropagationLossTwoWay[FreeSpace[r, ν]]

Out[26]=

(504850544566405639328987546634481 e^(4 π Im[r ν])/149896229 Abs[1/(r^2 ν^2)]^2)/(16 π^4)

In[27]:=

FullSimplify[PropagationLossTwoWay[FreeSpace[d, ν]], {d ∈ Reals, ν ∈ Reals}]

Out[27]=

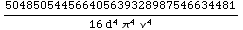
504850544566405639328987546634481/(16 d^4 π^4 ν^4)

In[28]:=

PropagationFactorOneWay[FreeSpace[{z1, z2, d}, Frequency[λ], SphereRadius :> a _ e, EarthRadiusScale -> 4/3]]

Out[28]=

(e^(-(2 i π ((z1 + (4 a _ e)/3)^2 - 2 Cos[(3 d)/(4 a _ e)] (z1 + (4 a _ e)/3) (z2 + (4 a ... 3)^2 - 2 Cos[(3 d)/(4 a _ e)] (z1 + (4 a _ e)/3) (z2 + (4 a _ e)/3) + (z2 + (4 a _ e)/3)^2)^(1/2))

•FreshWater

[Graphics:HTMLFiles/index_69.gif]

•FresnelIntegral

[Graphics:HTMLFiles/index_70.gif]

In[29]:=

FresnelIntegral[z]

Out[29]=

(1/2 - i/2) (1 - Erf[(1/2 + i/2) π^(1/2) z])

(1/2 - i/2) (1 - Erf[(1/2 + i/2) π^(1/2) z])

•HeightGainSphericalDiffraction

[Graphics:HTMLFiles/index_74.gif]

Usage message for HeightGainSphericalDiffraction

•IndexOfRefractionModelExponential

[Graphics:HTMLFiles/index_75.gif]

In[31]:=

IndexOfRefractionModelExponential[h, ρ, γ]

Out[31]=

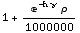
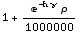
1 + (e^(-h γ) ρ)/1000000

1 + (e^(-h γ) ρ)/1000000

•IndexOfRefractionModelTropospheric

[Graphics:HTMLFiles/index_79.gif]

In[32]:=

IndexOfRefractionModelTropospheric[T, p, p _ H2O]

Out[32]=

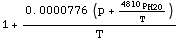
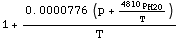
1 + (0.00007759999999999999` (p + (4810 p _ H2O)/T))/T

1 + (0.00007759999999999999` (p + (4810 p _ H2O)/T))/T

•KnifeEdgeDiffractionFourRay

[Graphics:HTMLFiles/index_83.gif]

Implementation not yet complete for this function.

In[33]:=

Abs @ N[PropagationFactorOneWay[KnifeEdgeDiffractionFourRay[30, 100, 20 KilometersToMeters, 5 KilometersToMeters, 400, 1100 MHz, ElectromagneticProperties[LoamySoil, 1100 Mhz]]]]

Out[33]=

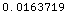
0.016371872603180005`

In[34]:=

Abs @ N[PropagationFactorOneWay[KnifeEdgeDiffraction[30, 100, 20 KilometersToMeters, 5 KilometersToMeters, 400, 1100 MHz]]]

Out[34]=

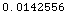
0.014255576985014798`

In[35]:=

Abs @ N[PropagationFactorOneWay[Multipath[30, 100, 20 KilometersToMeters, 1100 MHz, ElectromagneticProperties[LoamySoil, 1100 Mhz]]]]

Out[35]=

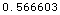
0.5666028123825452`

•KnifeEdgeDiffraction

[Graphics:HTMLFiles/index_90.gif]

In[36]:=

PropagationFactorOneWay[KnifeEdgeDiffraction[TransmitterHeight, TargetHeight, TransmitterToTargetDistance, TransmitterToKnifeEdgeDistance, KnifeEdgeHeight, Frequency]]

Out[36]=

PropagationFactorOneWay[KnifeEdgeDiffraction[TransmitterHeight, TargetHeight, TransmitterToTargetDistance, TransmitterToKnifeEdgeDistance, KnifeEdgeHeight, Frequency]]

In[37]:=

PropagationFactorOneWay[KnifeEdgeDiffraction[15, h, 20 KilometersToMeters, 15 KilometersToMeters, 30, ν]]

Out[37]=

1/2 (1 - Erf[1/(1/ν^(1/2) Abs[31855043857/3750 + h]^(1/2)) ((25 + 25 i) (3 π Csc[187 ... 1855043857/3750 + h) Sin[18750000/31855043857] - (31855100107 Sin[56250000/31855043857])/3750)))])

1/2 (1 - Erf[1/(1/ν^(1/2) Abs[31855043857/3750 + h]^(1/2)) ((25 + 25 i) (3 π Csc[187 ... 1855043857/3750 + h) Sin[18750000/31855043857] - (31855100107 Sin[56250000/31855043857])/3750)))])

In[38]:=

Plot[Evaluate[PropagationLossOneWay[KnifeEdgeDiffraction[15, h, 20 KilometersToMeters, 15 Kilo ... ToMeters, 30, 1500 Mhz]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_97.gif]

In Db:

In[39]:=

Plot[Evaluate[TodB[PropagationLossOneWay[KnifeEdgeDiffraction[15, h, 20 KilometersToMeters, 15 ... oMeters, 30, 1500 Mhz]]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_99.gif]

•LoamySoil

[Graphics:HTMLFiles/index_100.gif]

•Multipath

[Graphics:HTMLFiles/index_101.gif]

For Loamy Soil:

In[40]:=

ElectromagneticProperties[LoamySoil, 1500 Mhz]

Out[40]=

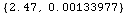
{2.47`, 0.0013397697487455636`}

In[41]:=

Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 Mhz, Ele ... [LoamySoil, 1500 Mhz]]]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_105.gif]

Determine when the transmitter and target are within line-of-sight of each other (HorizonDistance is contained in the package "Radar`RadarGeometry`"):

In[42]:=

? HorizonDistance

HorizonDistance[z] gives the distance to the horizon from a point at a height z over a sphere. ... However, for consistency, usage for the functions in this package should always default to meters.

In[43]:=

HorizonDistance[15] MetersToKilometers // N

Out[43]=

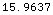
15.963708086048335`

In[44]:=

Plot[HorizonDistance[15, h] MetersToKilometers, {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_111.gif]

In[45]:=

FindRoot[HorizonDistance[15, h] MetersToKilometers == 20, {h, 10}]

Out[45]=

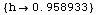
{h -> 0.9589329491179569`}

So the target is within line-of-sight once it is approximately a meter above the ground at this 20 Km distance.

In[46]:=

Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 Mhz, Ele ... [LoamySoil, 1500 Mhz]]]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_115.gif]

In[47]:=

DensityPlot[TodB[PropagationLossOneWay[Multipath[15, h, d KilometersToMeters, 1500 Mhz, Electr ... ue, FrameLabel -> {"Down Range", "Target Height"}, AspectRatio -> 1/2] ;

[Graphics:HTMLFiles/index_117.gif]

A contour plot that includes a free space propagation factor using a different color function:

In[48]:=

ContourPlot[TodB[PropagationLossOneWay[Multipath[15, h, d KilometersToMeters, 1500 Mhz, Electr ... nction -> (Hue[(# + 140)/40] &), ColorFunctionScaling -> False, AspectRatio -> 1/2] ;

[Graphics:HTMLFiles/index_119.gif]

Transmitter at 100 feet, target at 200 feet, frequency 3 GHz; plot for one-way propagation loss as a function transmitter to target distance. The geometrical horizon for this system is at (in nautical miles):

In[49]:=

hDistance = N[MetersToNauticalMiles HorizonDistance[100 FeetToMeters, 200 FeetToMeters]]

Out[49]=

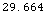
29.6639938432278`

In[50]:=

theplot = Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[100 FeetToMeters, 200 FeetToMeter ... (dB)"}, PlotRange -> {All, {-50, 10}}, Axes -> False, DisplayFunction -> Identity] ;

In[51]:=

Show[theplot, Graphics[{ AbsoluteThickness[2], RGBColor[1, 0, 0], Line[{{hDistance, -100}, ... e", {hDistance, 0}, {1, 0}]}], ImageSize -> 400, DisplayFunction -> $DisplayFunction] ;

[Graphics:HTMLFiles/index_124.gif]

Here is an example using the UseRoughnessFactor Option.

RoughnessFactorGaussian:

In[52]:=

plot1 = Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 ... essFactorGaussian, 2}]]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_126.gif]

RoughnessFactorGeneralized:

In[53]:=

Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 Mhz, Ele ... FactorGeneralized, 2}]]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_128.gif]

Here is an example using the UseDivergenceFactor Option.

In[54]:=

plot2 = Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 ... 0}, Frame -> True, PlotRange -> All, Axes -> False, PlotStyle -> RGBColor[0, 0, .6]] ;

[Graphics:HTMLFiles/index_130.gif]

And with a roughness factor and a divergence factor:

In[55]:=

plot3 = Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 ... 0}, Frame -> True, PlotRange -> All, Axes -> False, PlotStyle -> RGBColor[.6, 0, 0]] ;

[Graphics:HTMLFiles/index_132.gif]

In[56]:=

Show[plot1, plot2, plot3] ;

[Graphics:HTMLFiles/index_134.gif]

•Antenna patterns

In[57]:=

Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 Mhz, Ele ... [LoamySoil, 1500 Mhz]]]]], {h, 1, 350}, Frame -> True, PlotRange -> All, Axes -> False] ;

[Graphics:HTMLFiles/index_136.gif]

In[58]:=

ap = Evaluate[AntennaPattern[GaussianBeam[1/300, #, 0, 0 Degree]]] &

Out[58]=

2^(-1/2 Csc[1/300]^2 Sin[#1]^2) &

In[59]:=

ap2 = Evaluate[AntennaPattern[UniformLinearArray[20, λ/2, λ, #, 0, 0 Degree], Normalized -> True]] &

Out[59]=

1/20 Csc[1/2 π Sin[#1]] Sin[10 π Sin[#1]] &

In[60]:=

Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 Mhz, Ele ... me -> True, PlotRange -> All, Axes -> False, PlotPoints -> 40, Exchanged -> True] ;

[Graphics:HTMLFiles/index_142.gif]

In[61]:=

ElevationAngleGeometric[15, 13000, 20 KilometersToMeters]/Degree // N

Out[61]=

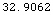
32.90615132044423`

In[62]:=

PolarAntennaPlot[AntennaPattern[UniformLinearArray[20, λ/2, λ, θ, 0, 0 Degree], Normalized -> True], {θ, -π, π}, PlotPoints -> 80] ;

[Graphics:HTMLFiles/index_146.gif]

In[63]:=

ContourPlot[TodB[PropagationLossOneWay[Multipath[15, h, d KilometersToMeters, 1500 Mhz, Electr ... nction -> (Hue[(# + 140)/40] &), ColorFunctionScaling -> False, AspectRatio -> 1/2] ;

[Graphics:HTMLFiles/index_148.gif]

In[64]:=

Plot[Evaluate[TodB[PropagationLossOneWay[Multipath[15, h, 20 KilometersToMeters, 1500 Mhz, Ele ... ]], {h, 1, 1000}, Frame -> True, PlotRange -> All, Axes -> False, Exchanged -> True] ;

[Graphics:HTMLFiles/index_150.gif]

In[65]:=

PropagationFactorOneWay[Multipath[15., 150, 20 KilometersToMeters, 1500 Mhz, ElectromagneticProperties[LoamySoil, 1500 Mhz]], ap]

Out[65]=

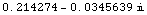
0.2142739195810578` - 0.03456391121617847` i

•OutOfLineOfSightDefault

[Graphics:HTMLFiles/index_153.gif]

In[66]:=

PackagesAndFunctionsWithOption[OutOfLineOfSightDefault]

Out[66]//DisplayForm=

[Graphics:HTMLFiles/index_155.gif]

•PadeDegree

In[67]:=

UsageMessageCell[PadeDegree, UsagesOnly -> True]

[Graphics:HTMLFiles/index_157.gif]

Usage message for PadeDegree

•PropagationFactorOneWay

[Graphics:HTMLFiles/index_158.gif]

•PropagationFactorTwoWay

[Graphics:HTMLFiles/index_159.gif]

•PropagationLossOneWay

[Graphics:HTMLFiles/index_160.gif]

•PropagationLossTwoWay

[Graphics:HTMLFiles/index_161.gif]

•Propagation

[Graphics:HTMLFiles/index_162.gif]

•PureWaterModelEMProperties

[Graphics:HTMLFiles/index_163.gif]

In[68]:=

PureWaterModelEMProperties[1500 MHz, FarenheitToKelvin[45]]

Out[68]=

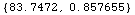
{83.74715391610295`, 0.8576550201353743`}

In[69]:=

FindRoot[PureWaterModelEMProperties[1500 MHz, FarenheitToKelvin[t]][[1]] == 78, {t, {30, 35}}]

Out[69]=

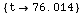
{t -> 76.0139909603718`}

In[70]:=

PureWaterModelEMProperties[1500 MHz, FarenheitToKelvin[76]]

Out[70]=

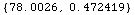
{78.00264068409989`, 0.4724191198762394`}

In[71]:=

ElectromagneticProperties[FreshWater, 1500 Mhz]

Out[71]=

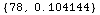
{78, 0.10414404524661869`}

•ReflectionCoefficient

[Graphics:HTMLFiles/index_172.gif]

In[72]:=

ReflectionCoefficient[ν, φ, {ϵ, σ}, VPol]

Out[72]=

(-(ϵ - (22468879468420441 i σ)/(1250000 ν) - Cos[φ]^2)^(1/2) + (ϵ - ... ;) - Cos[φ]^2)^(1/2) + (ϵ - (22468879468420441 i σ)/(1250000 ν)) Sin[φ])

In[73]:=

ReflectionCoefficient[ν, φ, {ϵ, σ}, HPol]

Out[73]=

(-(ϵ - (22468879468420441 i σ)/(1250000 ν) - Cos[φ]^2)^(1/2) + Sin[φ])/((ϵ - (22468879468420441 i σ)/(1250000 ν) - Cos[φ]^2)^(1/2) + Sin[φ])

Absolute value of the reflection coefficient for vertical polarization over sea water at 20° Celsius for frequencies of 100 MHz, 500 MHz, and 1 GHz.

In[74]:=

refCoeffV100 = Abs[ReflectionCoefficient[100 MHz, φ, SalineWaterModelEMProperties[100 MHz ... efficient[1000 MHz, φ, SalineWaterModelEMProperties[1000 MHz, CelsiusToKelvin[20]], VPol]] ;

In[77]:=

Plot[{refCoeffV100, refCoeffV500, refCoeffV1000}, {φ, 0, π/8}, Frame -> True, Plo ... 0, 0], RGBColor[0, 1, 0], RGBColor[1, 0, 1]}, PlotLabel -> "Vertical Polarization"] ;

[Graphics:HTMLFiles/index_179.gif]

Absolute value of the reflection coefficient for vertical polarization over sea water at 20° Celsius for frequencies of 100 MHz, 500 MHz, and 1 GHz.

In[78]:=

refCoeffH100 = Abs[ReflectionCoefficient[100 MHz, φ, SalineWaterModelEMProperties[100 MHz ... efficient[1000 MHz, φ, SalineWaterModelEMProperties[1000 MHz, CelsiusToKelvin[20]], HPol]] ;

In[81]:=

Plot[{refCoeffH100, refCoeffH500, refCoeffH1000}, {φ, 0, π/8}, Frame -> True, Plo ... 0], RGBColor[0, 1, 0], RGBColor[1, 0, 1]}, PlotLabel -> "Horizontal Polarization"] ;

[Graphics:HTMLFiles/index_182.gif]

•RefractivityModelExponential

[Graphics:HTMLFiles/index_183.gif]

In[82]:=

RefractivityModelExponential[h, r, γ]

Out[82]=

e^(-h γ) r

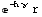
•RefractivityModelTropospheric

[Graphics:HTMLFiles/index_186.gif]

In[83]:=

RefractivityModelTropospheric[T, P, P _ H2O]

Out[83]=

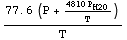
(77.6` (P + (4810 P _ H2O)/T))/T

•RoughnessFactorGaussian

[Graphics:HTMLFiles/index_189.gif]

In[84]:=

RoughnessFactorGaussian[σ _ h, ν, φ]

Out[84]=

e^(-(2 π^2 ν^2 Sin[φ]^2 σ _ h^2)/22468879468420441)

•RoughnessFactorGeneralized

[Graphics:HTMLFiles/index_192.gif]

In[85]:=

RoughnessFactorGeneralized[σ _ h, ν, φ]

Out[85]=

e^(-(2 π^2 ν^2 Sin[φ]^2 σ _ h^2)/22468879468420441) BesselI[0, (2 π^2 ν^2 Sin[φ]^2 σ _ h^2)/22468879468420441]

•SalineWaterModelEMProperties

[Graphics:HTMLFiles/index_195.gif]

In[86]:=

SalineWaterModelEMProperties[1500 MHz, FarenheitToKelvin[45]]

Out[86]=

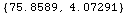
{75.85893600483084`, 4.072907475168566`}

In[87]:=

FindRoot[SalineWaterModelEMProperties[1500 MHz, FarenheitToKelvin[t]][[1]] == 75, {t, {30, 35}}]

Out[87]=

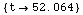
{t -> 52.06401948592587`}

In[88]:=

SalineWaterModelEMProperties[1500 MHz, FarenheitToKelvin[52]]

Out[88]=

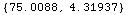
{75.00881236958372`, 4.319366572570795`}

In[89]:=

ElectromagneticProperties[SeaWater, 1500 Mhz]

Out[89]=

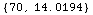
{70, 14.019390706275592`}

•SandySoil

[Graphics:HTMLFiles/index_204.gif]

•SeaIce

[Graphics:HTMLFiles/index_205.gif]

•SeaWater

[Graphics:HTMLFiles/index_206.gif]

•SnowFreshPacked

[Graphics:HTMLFiles/index_207.gif]

•SnowTightlyPacked

[Graphics:HTMLFiles/index_208.gif]

•SphericalDiffraction

[Graphics:HTMLFiles/index_209.gif]

This propagation model is of specific interest for so-called "surface wave" radar systems.

In[90]:=

sphericalLoss1 = PropagationLossOneWay[SphericalDiffraction[h1, h2, d, 2 Mhz, SalineWaterModelEMProperties[2 Mhz, FarenheitToKelvin[45]], 1]]

Out[90]=

0.00004492732486116416` e^(2 Re[(-5.621162550967793`*^-6 - 5.38797149784523`*^-6 i) d]) Abs[d^ ... 7249` h2] + AiryBi[(0.8135861139913326` - 0.8487980676557881` i) - 0.0007451101156037249` h2])]^2

In[91]:=

sphericalLoss2 = PropagationLossOneWay[SphericalDiffraction[h1, h2, d, 2 Mhz, SalineWaterModelEMProperties[2 Mhz, FarenheitToKelvin[45]], 10]]

Out[91]=

0.00008322075012977467` Abs[d^(1/2) ((-0.20429717906139983` + 0.7057761027821096` i) e^((-5.62 ... 7249` h2] + AiryBi[(6.217867170605868` - 10.718818913291429` i) - 0.0007451101156037249` h2]))]^2

In[92]:=

z1 = 40 ; z2 = 20 ; f = 2000 Mhz ; nterms = 200 ; polar = HPol ; hDistance = N[MetersToNautic ... ImageSize -> 400, DisplayFunction -> $DisplayFunction, PlotRange -> {All, {-100, 10}}] ;

[Graphics:HTMLFiles/index_215.gif]

•SurfaceTypes

[Graphics:HTMLFiles/index_216.gif]

In[102]:=

SurfaceTypes[]

Out[102]=

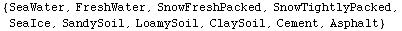
{SeaWater, FreshWater, SnowFreshPacked, SnowTightlyPacked, SeaIce, SandySoil, LoamySoil, ClaySoil, Cement, Asphalt}

•UseDivergenceFactor

[Graphics:HTMLFiles/index_219.gif]

In[103]:=

PackagesAndFunctionsWithOption[UseDivergenceFactor]

Out[103]//DisplayForm=

[Graphics:HTMLFiles/index_221.gif]

•UseRoughnessFactor

[Graphics:HTMLFiles/index_222.gif]

In[104]:=

PackagesAndFunctionsWithOption[UseRoughnessFactor]

Out[104]//DisplayForm=

[Graphics:HTMLFiles/index_224.gif]

For further information on our services send email to info@scientificarts.com .
Contents of this web site Copyright © 1999-2011, Scientific Arts, LLC.

d