Home

Staff
     
Consulting
               
Mathematica Tools

Customer Quotes
        
Contact

Older Mathematica Items
 

 

 

 

 

Scientific Arts

Detection

•Functions and parameters contained in this package:

In[1]:=

PackageFunctions[Detection, 2]

Out[1]//DisplayForm=

[Graphics:HTMLFiles/index_2.gif]

•Package functions and their basic documentation along with simple examples

•BinaryDetectorOptimalM

In[2]:=

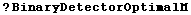
? BinaryDetectorOptimalM

BinaryDetectorOptimalM[DetectionModel, n, Pfa]

[Graphics:HTMLFiles/index_5.gif]

In[3]:=

BinaryDetectorOptimalM[Swerling0, 20, 1/10^5]

Out[3]=

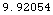
9.920539036127376`

In[4]:=

BinaryDetectorOptimalM[Swerling2, 20, 1/10^5]

Out[4]=

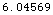
6.045687486017352`

•BinaryDetectorProbabilityFunction

[Graphics:HTMLFiles/index_10.gif]

In[5]:=

BinaryDetectorProbabilityFunction[n, m, p]

Out[5]=

(1 - p)^(-m + n) p^m Binomial[n, m] Gamma[1 + m] Hypergeometric2F1Regularized[1, m - n, 1 + m, p/(-1 + p)]

•BinaryDetectorSinglePulsePfa

[Graphics:HTMLFiles/index_13.gif]

In[6]:=

BinaryDetectorSinglePulsePfa[5, 2, 10^-6]

Out[6]=

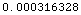
0.0003163278213937246`

•BinaryDetector

[Graphics:HTMLFiles/index_16.gif]

In[7]:=

DetectionProbability[{BinaryDetector[SwerlingModel2, 4], 5}, {3, 1/100000}]

Out[7]=

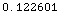
0.12260079832958266`

•CentralMomentsToLaplaceCharacteristicFunction

[Graphics:HTMLFiles/index_19.gif]

In[8]:=

CentralMomentsToLaplaceCharacteristicFunction[{σ^2, κ}, μ, λ]

Out[8]=

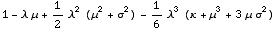
1 - λ μ + 1/2 λ^2 (μ^2 + σ^2) - 1/6 λ^3 (κ + μ^3 + 3 μ σ^2)

•Central

[Graphics:HTMLFiles/index_22.gif]

In[9]:=

PackagesAndFunctionsWithOption[MomentMethod]

Out[9]//DisplayForm=

[Graphics:HTMLFiles/index_24.gif]

•CentralToNonCentral

[Graphics:HTMLFiles/index_25.gif]

In[10]:=

CentralToNonCentral[2]

Out[10]=

-MomentNonCentral[1]^2 + MomentNonCentral[2]

In[11]:=

CentralToNonCentral[2, m]

Out[11]=

-m[1]^2 + m[2]

This can be expressed in a more conventional form by writing μ for the mean and σ for the standard deviation.  We then use an abbreviated notation for higher order central moments: κ _ i

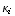
In[12]:=

Clear[σ, μ] ; m[1] := μ ; m[2] := σ^2 ; m[i_] := ν _ i ; CentralToNonCentral[2, m]

Out[16]=

-μ^2 + σ^2

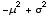
In[17]:=

CentralToNonCentral[3, m]

Out[17]=

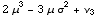
2 μ^3 - 3 μ σ^2 + ν _ 3

Arbitraty higher order expressions can easilly be generated:

In[18]:=

CentralToNonCentral[15, m]

Out[18]=

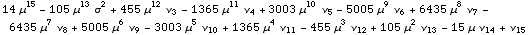
14 μ^15 - 105 μ^13 σ^2 + 455 μ^12 ν _ 3 - 1365 μ^11 ν _ 4 + ... ; _ 11 - 455 μ^3 ν _ 12 + 105 μ^2 ν _ 13 - 15 μ ν _ 14 + ν _ 15

One practical purpose of this function is to transform data taken for the moments of a distribution from one form to another.  For example the data may be from explicit measurements of the pulse-to-pulse fluctuations of the radar cross section of a realistic target. These data can then be used to construct the LaplaceCharacteristicFunction for this target (using CentralMomentsToLaplaceCharacteristicFunction) which is then used in the EdgeworthDetectionExpansion or the EdgeworthProbabilityExpansion to construct a detection model for this target (using MakeEdgeworthDetectionExpansion or MakeEdgeworthDetectionExpansionCode).

•ChiSquareModel

[Graphics:HTMLFiles/index_37.gif]

•CoherentDetector

[Graphics:HTMLFiles/index_38.gif]

•CoherentDetectorFunction

[Graphics:HTMLFiles/index_39.gif]

Usage message for CoherentDetectorFunction

•CorrelationMatrix

[Graphics:HTMLFiles/index_40.gif]

In[19]:=

CorrelationMatrix[CorrelationFunction, 2]

Out[19]=

CorrelationMatrix[CorrelationFunction, 2]

In[20]:=

CorrelationMatrix[χ[#1, #2] &, 3] // MatrixForm

Out[20]//MatrixForm=

( χ[1, 1] χ[1, 2] χ[1, 3] ) χ[2, 1] χ[2, 2] χ[2, 3] χ[3, 1] χ[3, 2] χ[3, 3]

•Cumulant

[Graphics:HTMLFiles/index_45.gif]

In[21]:=

Cumulant[9, m]

Out[21]=

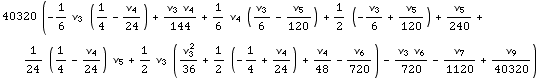
40320 (-1/6 ν _ 3 (1/4 - ν _ 4/24) + (ν _ 3 ν _ 4)/144 + 1/6 ν _ 4 (& ... #957; _ 4/48 - ν _ 6/720) - (ν _ 3 ν _ 6)/720 - ν _ 7/1120 + ν _ 9/40320)

•DetectionModels

[Graphics:HTMLFiles/index_48.gif]

In[22]:=

DetectionModels[]

Out[22]=

{ChiSquareModel, MarcumModel, SwerlingModel0, RiceModel, SwerlingModel0, SwerlingModel1, SwerlingModel2, SwerlingModel3, SwerlingModel4, SwerlingModel5}

•DetectionProbabilityCalculator

[Graphics:HTMLFiles/index_51.gif]

In[16]:=

DetectionProbabilityCalculator[]

Out[16]=

NotebookObject[<< Detection Probability Calculator >>]

[Graphics:HTMLFiles/index_54.gif]

•DetectionProbabilityReport

[Graphics:HTMLFiles/index_55.gif]

In[24]:=

DetectionProbabilityReport[{5}, {5.0, 10^(-3)}]

[Graphics:HTMLFiles/index_57.gif]

•DetectionProbability

[Graphics:HTMLFiles/index_58.gif]

Coherent Detector

In[25]:=

DetectionProbability[{CoherentDetector, 1}, {snr, pfa}]

Out[25]=

DetectionProbability[{CoherentDetector, 1}, {snr, pfa}]

In[26]:=

DetectionProbability[{CoherentDetector, 2}, {snr, pfa}]

Out[26]=

DetectionProbability[{CoherentDetector, 2}, {snr, pfa}]

In[27]:=

DetectionProbability[{CoherentDetector, 3}, {snr, pfa}]

Out[27]=

DetectionProbability[{CoherentDetector, 3}, {snr, pfa}]

Swerling 0

In[28]:=

DetectionProbability[{SwerlingModel0, 1}, {snr, pfa}]

Out[28]=

MarcumQProbabilityFunction[1, snr, -Log[pfa], {ComputationMethod -> Automatic}]

In[29]:=

DetectionProbability[{SwerlingModel0, 2}, {snr, pfa}]

Out[29]=

MarcumQProbabilityFunction[2, snr, -1 - ProductLog[-1, -pfa/e], {ComputationMethod -> Automatic}]

In[30]:=

DetectionProbability[{SwerlingModel0, 3}, {snr, pfa}]

Out[30]=

MarcumQProbabilityFunction[3, snr, DetectionThreshold[{SquareLawDetector, 3}, pfa], {ComputationMethod -> Automatic}]

Swerling 1

In[31]:=

DetectionProbability[{SwerlingModel1, 1}, {snr, pfa}]

Out[31]=

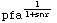
pfa^1/(1 + snr)

In[32]:=

DetectionProbability[{SwerlingModel1, 2}, {snr, pfa}]

Out[32]=

(e^(1 + ProductLog[-1, -pfa/e]) (-1 + e^(2 snr (-1 - ProductLog[-1, -pfa/e]))/(1 + 2 snr) (1 + 2 snr)))/(2 snr)

In[33]:=

DetectionProbability[{SwerlingModel1, 3}, {snr, pfa}]

Out[33]=

GammaRegularized[2, DetectionThreshold[{SquareLawDetector, 3}, pfa]] + e^(-DetectionThreshold[ ... snr))^2 (1 - GammaRegularized[2, DetectionThreshold[{SquareLawDetector, 3}, pfa]/(1 + 1/(3 snr))])

Swerling 2

In[34]:=

DetectionProbability[{SwerlingModel2, 1}, {snr, pfa}]

Out[34]=

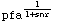
pfa^1/(1 + snr)

In[35]:=

DetectionProbability[{SwerlingModel2, 2}, {snr, pfa}]

Out[35]=

GammaRegularized[2, (-1 - ProductLog[-1, -pfa/e])/(1 + snr)]

In[36]:=

DetectionProbability[{SwerlingModel2, 3}, {snr, pfa}]

Out[36]=

GammaRegularized[3, DetectionThreshold[{SquareLawDetector, 3}, pfa]/(1 + snr)]

Swerling 3

In[37]:=

DetectionProbability[{SwerlingModel3, 1}, {snr, pfa}]

Out[37]=

pfa^1/(1 + snr/2) (1 - (2 snr Log[pfa])/(2 + snr)^2)

In[38]:=

DetectionProbability[{SwerlingModel3, 2}, {snr, pfa}]

Out[38]=

e^(-(-1 - ProductLog[-1, -pfa/e])/(1 + snr)) (1 + (-1 - ProductLog[-1, -pfa/e])/(1 + snr))

In[39]:=

DetectionProbability[{SwerlingModel3, 3}, {snr, pfa}]

Out[39]=

e^(-DetectionThreshold[{SquareLawDetector, 3}, pfa]/(1 + (3 snr)/2)) (1 + 2/(3 snr)) (1 - 2/(3 snr) + DetectionThreshold[{SquareLawDetector, 3}, pfa]/(1 + (3 snr)/2))

Swerling 4

In[40]:=

DetectionProbability[{SwerlingModel4, 1}, {snr, pfa}]

Out[40]=

pfa^1/(1 + snr/2) (1 - (2 snr Log[pfa])/(2 + snr)^2)

In[41]:=

DetectionProbability[{SwerlingModel4, 2}, {snr, pfa}]

Out[41]=

1 - 1/(1 + snr/2)^2 (2 (1/2 (1 - GammaRegularized[2, (-1 - ProductLog[-1, -pfa/e])/(1 + snr/2) ... )/(1 + snr/2)]) + 1/8 snr^2 (1 - GammaRegularized[4, (-1 - ProductLog[-1, -pfa/e])/(1 + snr/2)])))

In[42]:=

DetectionProbability[{SwerlingModel4, 3}, {snr, pfa}]

Out[42]=

1 - 1/(1 + snr/2)^3 (6 (1/6 (1 - GammaRegularized[3, DetectionThreshold[{SquareLawDetector, 3} ... /48 snr^3 (1 - GammaRegularized[6, DetectionThreshold[{SquareLawDetector, 3}, pfa]/(1 + snr/2)])))

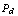P _ d versus snr at a value of 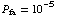P _ fa = 10^(-5) for a single pulse:

In[43]:=

WeibullPlot[Evaluate[DetectionProbability[{SwerlingModel4, 1}, {snr, 10^(-5)}]], {snr, 1, 20}, Frame -> True, Axes -> False, FrameLabel -> {SNR, Pd}, AspectRatio -> GoldenRatio] ;

[Graphics:HTMLFiles/index_98.gif]

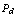P _ d versus snr at a value of 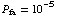P _ fa = 10^(-5) for a 10 pulses:

In[44]:=

WeibullPlot[Evaluate[DetectionProbability[{SwerlingModel4, 10}, {snr, 10^(-5)}]], {snr, 1, 20}, Frame -> True, Axes -> False, FrameLabel -> {SNR, Pd}, AspectRatio -> GoldenRatio] ;

[Graphics:HTMLFiles/index_102.gif]

•Detection

[Graphics:HTMLFiles/index_103.gif]

•DetectionThreshold

[Graphics:HTMLFiles/index_104.gif]

In[45]:=

DetectionThreshold[{SquareLawDetector, 4}, 10^(-3)]

Out[45]=

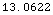
13.062240779188071`

In[46]:=

DetectionThreshold[{CoherentDetector, 4}, 10^(-3)] // N

Out[46]=

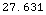
27.63102111592855`

In[47]:=

DetectionThreshold[{BinaryDetector[4], 4}, 10^(-3)]

Out[47]=

(3 Log[10])/4

•Detectors

[Graphics:HTMLFiles/index_111.gif]

In[48]:=

Detectors[]

Out[48]=

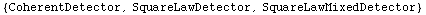
{CoherentDetector, SquareLawDetector, SquareLawMixedDetector}

•EdgeworthCumulativeExpansion

[Graphics:HTMLFiles/index_114.gif]

In[49]:=

EdgeworthCumulativeExpansion[2, t]

Out[49]=

1/2 (1 + Erf[t/2^(1/2)])

In[50]:=

EdgeworthCumulativeExpansion[3, t]

Out[50]=

1/2 (1 + Erf[t/2^(1/2)]) - (e^(-t^2/2) (-2 + 2 t^2) MomentCentral[3])/(12 (2 π)^(1/2))

In[51]:=

EdgeworthCumulativeExpansion[4, t]

Out[51]=

(e^(-t^2/2) (-6 2^(1/2) t + 2 2^(1/2) t^3))/(32 π^(1/2)) + 1/2 (1 + Erf[t/2^(1/2)]) - (e^ ... 576 π^(1/2)) - (e^(-t^2/2) (-6 2^(1/2) t + 2 2^(1/2) t^3) MomentCentral[4])/(96 π^(1/2))

•EdgeworthDetectionExpansion

[Graphics:HTMLFiles/index_121.gif]

In[52]:=

EdgeworthDetectionExpansion[1, t]

Out[52]=

1 + 1/2 (-1 - Erf[t/2^(1/2)])

In[53]:=

EdgeworthDetectionExpansion[2, t]

Out[53]=

1 + 1/2 (-1 - Erf[t/2^(1/2)])

In[54]:=

EdgeworthDetectionExpansion[3, t]

Out[54]=

1 + 1/2 (-1 - Erf[t/2^(1/2)]) + (e^(-t^2/2) (-2 + 2 t^2) MomentCentral[3])/(12 (2 π)^(1/2))

•EdgeworthProbabilityExpansion

[Graphics:HTMLFiles/index_128.gif]

In[55]:=

EdgeworthDetectionExpansion[1, t]

Out[55]=

1 + 1/2 (-1 - Erf[t/2^(1/2)])

In[56]:=

EdgeworthDetectionExpansion[2, t]

Out[56]=

1 + 1/2 (-1 - Erf[t/2^(1/2)])

In[57]:=

EdgeworthDetectionExpansion[3, t]

Out[57]=

1 + 1/2 (-1 - Erf[t/2^(1/2)]) + (e^(-t^2/2) (-2 + 2 t^2) MomentCentral[3])/(12 (2 π)^(1/2))

•EdgeworthTerms

[Graphics:HTMLFiles/index_135.gif]

In[58]:=

EdgeworthTerms[k, Phi, semiInvariant]

Out[58]=

EdgeworthTerms[k, Phi, semiInvariant]

In[59]:=

EdgeworthTerms[3, Phi, semiInvariant]

Out[59]=

Phi[0] - 1/6 Phi[3] semiInvariant[3]

•ExponentialCorrelationMatrix

[Graphics:HTMLFiles/index_140.gif]

In[60]:=

ExponentialCorrelationMatrix[α, 4] // MatrixForm

Out[60]//MatrixForm=

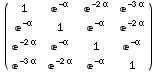
( -α -2 α -3 α ) 1 e e ... 1 e -3 α -2 α -α e e e 1

•FalseAlarmNumberToFalseAlarmProbability

[Graphics:HTMLFiles/index_143.gif]

In[61]:=

FalseAlarmNumberToFalseAlarmProbability[n _ fa]

Out[61]=

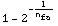
1 - 2^(-1/n _ fa)

•FalseAlarmProbability

[Graphics:HTMLFiles/index_146.gif]

In[62]:=

FalseAlarmProbability[{SquareLawDetector, 4}, τ]

Out[62]=

GammaRegularized[4, τ]

In[63]:=

FalseAlarmProbability[{CoherentDetector, 4}, τ]

Out[63]=

e^(-τ/4)

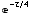
•FalseAlarmProbabilityToFalseAlarmNumber

[Graphics:HTMLFiles/index_151.gif]

In[64]:=

FalseAlarmProbabilityToFalseAlarmNumber[p _ fa]

Out[64]=

-Log[2]/Log[1 - p _ fa]

•GammaExpansion

[Graphics:HTMLFiles/index_154.gif]

In[65]:=

PackagesAndFunctionsWithOption[ComputationMethod]

Out[65]//DisplayForm=

[Graphics:HTMLFiles/index_156.gif]

•GaussianCorrelationMatrix

[Graphics:HTMLFiles/index_157.gif]

In[66]:=

GaussianCorrelationMatrix[α, 4] // MatrixForm

Out[66]//MatrixForm=

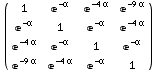
( -α -4 α -9 α ) 1 e e ... 1 e -9 α -4 α -α e e e 1

•GCFunction

[Graphics:HTMLFiles/index_160.gif]

In[67]:=

PackagesAndFunctionsWithOption[GCFunction]

Out[67]//DisplayForm=

[Graphics:HTMLFiles/index_162.gif]

•GramCharlierCumulativeExpansion

[Graphics:HTMLFiles/index_163.gif]

In[68]:=

GramCharlierCumulativeExpansion[1, t]

Out[68]=

1/2 (1 + Erf[t/2^(1/2)])

In[69]:=

GramCharlierCumulativeExpansion[2, t]

Out[69]=

1/2 (1 + Erf[t/2^(1/2)])

In[70]:=

GramCharlierCumulativeExpansion[3, t]

Out[70]=

1/2 (1 + Erf[t/2^(1/2)]) - (e^(-t^2/2) (-1 + t^2) MomentCentral[3])/(6 (2 π)^(1/2))

•GramCharlierDetectionExpansion

[Graphics:HTMLFiles/index_170.gif]

In[71]:=

GramCharlierDetectionExpansion[1, t]

Out[71]=

1 + 1/2 (-1 - Erf[t/2^(1/2)])

In[72]:=

GramCharlierDetectionExpansion[2, t]

Out[72]=

1 + 1/2 (-1 - Erf[t/2^(1/2)])

In[73]:=

GramCharlierDetectionExpansion[3, t]

Out[73]=

1 + 1/2 (-1 - Erf[t/2^(1/2)]) + (e^(-t^2/2) (-1 + t^2) MomentCentral[3])/(6 (2 π)^(1/2))

•GramCharlierFunction

[Graphics:HTMLFiles/index_177.gif]

In[74]:=

GramCharlierFunction[1, t]

Out[74]=

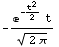
-(e^(-t^2/2) t)/(2 π)^(1/2)

In[75]:=

GramCharlierFunction[2, t]

Out[75]=

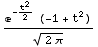
(e^(-t^2/2) (-1 + t^2))/(2 π)^(1/2)

In[76]:=

GramCharlierFunction[3, t]

Out[76]=

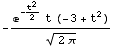
-(e^(-t^2/2) t (-3 + t^2))/(2 π)^(1/2)

•GramCharlierProbabilityExpansion

[Graphics:HTMLFiles/index_184.gif]

In[77]:=

GramCharlierProbabilityExpansion[1, t]

Out[77]=

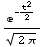
e^(-t^2/2)/(2 π)^(1/2)

In[78]:=

GramCharlierProbabilityExpansion[2, t]

Out[78]=

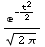
e^(-t^2/2)/(2 π)^(1/2)

In[79]:=

GramCharlierProbabilityExpansion[3, t]

Out[79]=

e^(-t^2/2)/(2 π)^(1/2) + (e^(-t^2/2) t (-3 + t^2) MomentCentral[3])/(6 (2 π)^(1/2))

•LaplaceCharacteristicFunction

[Graphics:HTMLFiles/index_191.gif]

In[80]:=

LaplaceCharacteristicFunction[{ModelType, NumberOfPulses}, SignalToNoiseRatio, LaplaceVariable]

Out[80]=

LaplaceCharacteristicFunction[{ModelType, NumberOfPulses}, SignalToNoiseRatio, LaplaceVariable]

In[81]:=

LaplaceCharacteristicFunction[{MarcumModel, n}, s, λ]

Out[81]=

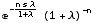
e^(-(n s λ)/(1 + λ)) (1 + λ)^(-n)

•LinearDetectorFunction

[Graphics:HTMLFiles/index_196.gif]

Usage message for LinearDetectorFunction

•MakeEdgeworthDetectionExpansionCode

[Graphics:HTMLFiles/index_197.gif]

In[82]:=

MakeEdgeworthDetectionExpansionCode[marcum, {LaplaceCharacteristicFunction[{MarcumModel, n}, s, λ], λ}, τ, 3]

[Graphics:HTMLFiles/index_199.gif]

•MakeEdgeworthDetectionExpansion

[Graphics:HTMLFiles/index_200.gif]

In[88]:=

MakeEdgeworthDetectionExpansion[{LaplaceCharacteristicFunction[{MarcumModel, n}, s, λ], λ}, τ, 1]

Out[88]=

1 + 1/2 (-1 - Erf[(-n (1 + s) + τ)/(2^(1/2) (n + 2 n s)^(1/2))])

In[89]:=

MakeEdgeworthDetectionExpansion[{LaplaceCharacteristicFunction[{MarcumModel, n}, s, λ], λ}, τ, 3]

Out[89]=

1 + (e^(-(-n (1 + s) + τ)^2/(2 (n + 2 n s))) (n + 3 n s) (-2 + (2 (-n (1 + s) + τ)^2 ... 960;)^(1/2) (n + 2 n s)^(3/2)) + 1/2 (-1 - Erf[(-n (1 + s) + τ)/(2^(1/2) (n + 2 n s)^(1/2))])

•MarcumModel

[Graphics:HTMLFiles/index_205.gif]

•Models

[Graphics:HTMLFiles/index_206.gif]

In[90]:=

PackagesAndFunctionsWithOption[Models]

Out[90]//DisplayForm=

[Graphics:HTMLFiles/index_208.gif]

•MomentCentral

[Graphics:HTMLFiles/index_209.gif]

•MomentFunction

[Graphics:HTMLFiles/index_210.gif]

In[91]:=

PackagesAndFunctionsWithOption[MomentFunction]

Out[91]//DisplayForm=

[Graphics:HTMLFiles/index_212.gif]

•MomentMethod

[Graphics:HTMLFiles/index_213.gif]

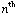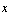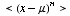The n^th central moment of a probability distribution of one varialbe x is < (x - μ)^n > where μ is the mean of the distribution.

The 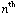n^th noncentral moment of a probability distribution of one varialbe 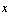x is < x^n > .

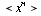In[92]:=

PackagesAndFunctionsWithOption[MomentMethod]

Out[92]//DisplayForm=

[Graphics:HTMLFiles/index_221.gif]

•MomentNonCentral

[Graphics:HTMLFiles/index_222.gif]

•NonCentralMomentsToLaplaceCharacteristicFunction

[Graphics:HTMLFiles/index_223.gif]

In[93]:=

NonCentralMomentsToLaplaceCharacteristicFunction[{ν _ 1, ν _ 2, ν _ 3}, λ]

Out[93]=

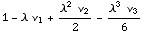
1 - λ ν _ 1 + (λ^2 ν _ 2)/2 - (λ^3 ν _ 3)/6

•NonCentral

[Graphics:HTMLFiles/index_226.gif]

•NonCentralToCentral

[Graphics:HTMLFiles/index_227.gif]

In[94]:=

NonCentralToCentral[2]

Out[94]=

MomentCentral[2] + MomentNonCentral[1]^2

In[95]:=

NonCentralToCentral[2, {c, μ}]

Out[95]=

c[2] + μ[1]^2

This can be expressed in a more concisely using an abbreviated notation for higher order central moments: 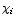χ _ i.

In[96]:=

Clear[σ, μ] ; μ[1] := μ ; c[i_] := χ _ i ; NonCentralToCentral[2, {c, μ}]

Out[99]=

μ^2 + χ _ 2

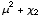
In[100]:=

NonCentralToCentral[3, {c, μ}]

Out[100]=

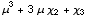
μ^3 + 3 μ χ _ 2 + χ _ 3

Arbitraty higher order expressions can easilly be generated:

In[101]:=

NonCentralToCentral[15, {c, μ}]

Out[101]=

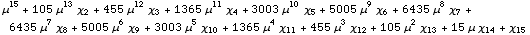
μ^15 + 105 μ^13 χ _ 2 + 455 μ^12 χ _ 3 + 1365 μ^11 χ _ 4 + ... ; _ 11 + 455 μ^3 χ _ 12 + 105 μ^2 χ _ 13 + 15 μ χ _ 14 + χ _ 15

As with the function CentralToNonCentral, one practical purpose of this function is to transform data taken for the moments of a distribution from one form to another.  For example the data may be from explicit measurements of the pulse-to-pulse fluctuations of the radar cross section of a realistic target. These data can then be used to construct the LaplaceCharacteristicFunction for this target (using CentralMomentsToLaplaceCharacteristicFunction) which is then used in the EdgeworthDetectionExpansion or the EdgeworthProbabilityExpansion to construct a detection model for this target (using MakeEdgeworthDetectionExpansion or MakeEdgeworthDetectionExpansionCode).

•NonFluctuatingModel

[Graphics:HTMLFiles/index_239.gif]

•PositiveIntegerOrExpressionQ

[Graphics:HTMLFiles/index_240.gif]

Usage message for PositiveIntegerOrExpressionQ

•PositiveOrExpressionQ

[Graphics:HTMLFiles/index_241.gif]

Usage message for PositiveOrExpressionQ

•ProbabilityOfDetection

[Graphics:HTMLFiles/index_242.gif]

Usage message for ProbabilityOfDetection

•ProbabilityOfFalseAlarm

[Graphics:HTMLFiles/index_243.gif]

Usage message for ProbabilityOfFalseAlarm

•ProbabilityOrExpressionQ

[Graphics:HTMLFiles/index_244.gif]

Usage message for ProbabilityOrExpressionQ

•ProbabilityQ

[Graphics:HTMLFiles/index_245.gif]

In[102]:=

ProbabilityQ[1.1]

Out[102]=

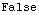
False

In[103]:=

ProbabilityQ[1/π]

Out[103]=

True

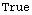
•ProbabilityQWithMessage

[Graphics:HTMLFiles/index_250.gif]

Usage message for ProbabilityQWithMessage

•PureSymbolOrExpressionQ

[Graphics:HTMLFiles/index_251.gif]

Usage message for PureSymbolOrExpressionQ

•RiceModel

[Graphics:HTMLFiles/index_252.gif]

•SemiInvariant

[Graphics:HTMLFiles/index_253.gif]

In[104]:=

SemiInvariant[6, m]

Out[104]=

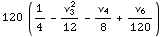
120 (1/4 - ν _ 3^2/12 - ν _ 4/8 + ν _ 6/120)

In[105]:=

Cumulant[6, m]

Out[105]=

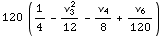
120 (1/4 - ν _ 3^2/12 - ν _ 4/8 + ν _ 6/120)

•SignalToNoiseReport

[Graphics:HTMLFiles/index_258.gif]

In[106]:=

SignalToNoiseReport[{5}, {.99, 10^(-5)}]

[Graphics:HTMLFiles/index_260.gif]

In[107]:=

SignalToNoise[{SwerlingModel1, 2}, {.99, 10^(-5)}] // TodB

Out[107]=

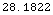
28.182244558006992`

•SignalToNoise

[Graphics:HTMLFiles/index_263.gif]

In[108]:=

SignalToNoise[{Swerling1, 1}, {pd, 10^(-5)}]

Out[108]=

-(Log[100000] + Log[pd])/Log[pd]

In[109]:=

SignalToNoise[{Swerling1, 1}, {.75, 10^(-5)}]

Out[109]=

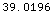
39.01961389825547`

In[110]:=

pd = DetectionProbability[{SwerlingModel1, 2}, {10, 10^(-5)}] // N

Out[110]=

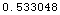
0.5330476014084444`

In[111]:=

SignalToNoise[{Swerling1, 2}, {pd, 10^(-5)}]

Out[111]=

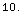
10.000000000000005`

In[112]:=

pd = DetectionProbability[{SwerlingModel1, 2}, {10, 10^(-5)}] // N

Out[112]=

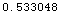
0.5330476014084444`

In[113]:=

Options[SignalToNoise]

Out[113]=

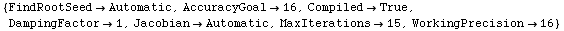
{FindRootSeed -> Automatic, AccuracyGoal -> 16, Compiled -> True, DampingFactor -> 1, Jacobian -> Automatic, MaxIterations -> 15, WorkingPrecision -> 16}

In[114]:=

SignalToNoise[{Swerling1, 1}, {9/10, 10^(-5)}]

Out[114]=

(-Log[10/9] + Log[100000])/Log[10/9]

•SquareLawDetectorFunction

[Graphics:HTMLFiles/index_278.gif]

In[135]:=

SquareLawDetectorFunction[{x1, x2}]

Out[135]=

Abs[x1]^2 + Abs[x2]^2

•SquareLawDetector

[Graphics:HTMLFiles/index_281.gif]

•SquareLawMixedDetector

[Graphics:HTMLFiles/index_282.gif]

•Swerling0

[Graphics:HTMLFiles/index_283.gif]

•Swerling1

[Graphics:HTMLFiles/index_284.gif]

•Swerling2

[Graphics:HTMLFiles/index_285.gif]

•Swerling3

[Graphics:HTMLFiles/index_286.gif]

•Swerling4

[Graphics:HTMLFiles/index_287.gif]

•Swerling5

[Graphics:HTMLFiles/index_288.gif]

•SwerlingCompute

[Graphics:HTMLFiles/index_289.gif]

•SwerlingModel0

[Graphics:HTMLFiles/index_290.gif]

•SwerlingModel1

[Graphics:HTMLFiles/index_291.gif]

•SwerlingModel2

[Graphics:HTMLFiles/index_292.gif]

•SwerlingModel3

[Graphics:HTMLFiles/index_293.gif]

•SwerlingModel4

[Graphics:HTMLFiles/index_294.gif]

•SwerlingModel5

[Graphics:HTMLFiles/index_295.gif]

For further information on our services send email to info@scientificarts.com .
Contents of this web site Copyright © 1999-2011, Scientific Arts, LLC.

d