Home

Staff
     
Consulting
               
Mathematica Tools

Customer Quotes
        
Contact

Older Mathematica Items
 

 

 

 

 

Scientific Arts

CrossSections

•Functions and parameters contained in this package:

In[1]:=

RadarPackageFunctions[CrossSections, 2]

Out[1]//DisplayForm=

[Graphics:HTMLFiles/index_2.gif]

•Package functions and their basic documentation along with simple examples

•CircularConductingCylinderRCS

[Graphics:HTMLFiles/index_3.gif]

In[2]:=

CircularConductingCylinderRCS[ν, l, a, θ]

Out[2]=

(149896229 a Sec[θ] Sin[(l π ν Cos[θ])/149896229]^2 Tan[θ])/(π ν)

•CrossSections

[Graphics:HTMLFiles/index_6.gif]

•EllipsoidRCS

[Graphics:HTMLFiles/index_7.gif]

In[3]:=

EllipsoidRCS[a, b, c, θ, φ]

Out[3]=

(a^2 b^2 c^2 π)/(c^2 Cos[θ]^2 + a^2 Cos[φ]^2 Sin[θ]^2 + b^2 Sin[θ]^2 Sin[φ]^2)^2

Prolate or oblate ellipsoid:

In[4]:=

EllipsoidRCS[a, a, b, θ, φ] // Simplify

Out[4]=

(4 a^4 b^2 π)/(a^2 + b^2 + (-a^2 + b^2) Cos[2 θ])^2

•FlatConductingCircularPlateRCS

[Graphics:HTMLFiles/index_12.gif]

In[5]:=

FlatConductingCircularPlateRCS[ν, a, θ]

Out[5]=

a^2 π BesselJ[1, (2 a π ν Sin[θ])/149896229]^2 Cot[θ]^2

•MieBackscatterSumScaled

[Graphics:HTMLFiles/index_15.gif]

For infinite conductivity there is no explicit dependence on the frequency.

In[6]:=

D[MieBackscatterSumScaled[ω, ρ, ∞, 3], ω]

Out[6]=

0

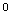
In[7]:=

tem = TodB[MieBackscatterSumScaled[ ρ,    10]] ;

With 10 terms in the Mie Series:

In[8]:=

Plot[Evaluate[TodB[MieBackscatterSumScaled[ ρ,    10]]], {ρ, .1, 10}, Frame -> True, FrameLabel -> {ρ, "Cross Section"}, PlotRange -> All] ;

[Graphics:HTMLFiles/index_20.gif]

With 20 terms in the Mie Series:

In[9]:=

Plot[Evaluate[TodB[MieBackscatterSumScaled[ ρ,    20]]], {ρ, .1, 10}, Frame -> True, FrameLabel -> {ρ, "Cross Section"}, PlotRange -> All] ;

[Graphics:HTMLFiles/index_22.gif]

Here is a comparison of the scaled backscatter cross section of a sphere with infinite conductivity with that of a sphere of low conductivity (the dielectric properties in the latter case are those of pure water at room temperature and at a frequency of 1 GHz)

This is a list of the dielectric constant and conductivity of pure water:

In[10]:=

waterEMProperties = PureWaterModelEMProperties[GHz, FarenheitToKelvin[65]]

Out[10]=

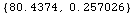
{80.43741581618424`, 0.2570255471761209`}

Here is log-log plot of these two cases, the pure water curve is given in red:

In[11]:=

nterms = 7 ; <br /> LogLogPlot[Evaluate[{MieBackscatterSumScaled[2 π ρ, nterms], <br ... Axes -> False, PlotStyle -> {RGBColor[0, 0, 0], RGBColor[1, 0, 0]}, PlotRange -> All] ;

[Graphics:HTMLFiles/index_26.gif]

•MieBackscatterSum

[Graphics:HTMLFiles/index_27.gif]

In[13]:=

MieBackscatterSum[3 GHz, 1, {ϵ, ∞}, 1]

Out[13]=

(22468879468420441 Abs[BesselJ[3/2, (3000000000 π)/149896229]/(BesselJ[3/2, (3000000000 & ... i π BesselY[5/2, (3000000000 π)/149896229])/149896229)]^2)/(1000000000000000000 π)

•ThinConductingStraightWireRCS

[Graphics:HTMLFiles/index_30.gif]

In[14]:=

ThinConductingStraightWireRCS[ν, l, a, θ, φ]

Out[14]=

(l^2 π Cos[φ]^4 Sin[θ]^2 Sin[(l π ν Cos[θ])/149896229]^2)/((2 - ... [θ])/299792458)^2 (π^2/4 + Log[(a e^EulerGamma π ν Sin[θ])/299792458]^2))

For further information on our services send email to info@scientificarts.com .
Contents of this web site Copyright © 1999-2011, Scientific Arts, LLC.

d