Home

Staff
     
Consulting
               
Mathematica Tools

Customer Quotes
        
Contact

Older Mathematica Items
 

 

 

 

 

Scientific Arts

Antennas

•Functions and parameters contained in this package:

In[29]:=

RadarPackageFunctions[Antennas, 2]

Out[29]//DisplayForm=

[Graphics:HTMLFiles/index_2.gif]

•Package functions and their basic documentation along with simple examples

•AntennaPattern

[Graphics:HTMLFiles/index_3.gif]

In[1]:=

Options[AntennaPattern]

Out[1]=

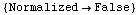
{Normalized -> False}

•Antennas

[Graphics:HTMLFiles/index_6.gif]

•AntennaTemperature

[Graphics:HTMLFiles/index_7.gif]

In[2]:=

AntennaTemperature[T _ T, T _ TL, L]

Out[2]=

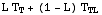
L T _ T + (1 - L) T _ TL

•ApertureExcitation

[Graphics:HTMLFiles/index_10.gif]

In[3]:=

ApertureExcitation[BaylissLineSource[r, nbar, d, λ, θ], x]

Out[3]=

Underoverscript[∑, K = 0, arg3] BaylissLineB[r, K, nbar] Sin[((2 π x) (K + 1/2))/d]

In[4]:=

ApertureExcitation[BaylissLineSource[FromdB[30], 5, d], x]

Out[4]=

0.26843876636826486` Sin[(π x)/d] + 0.1621540136819705` Sin[(3 π x)/d] - 0.008838209 ... 60; x)/d] + 0.002913038090281392` Sin[(7 π x)/d] - 0.0007027248993531724` Sin[(9 π x)/d]

In[5]:=

ae = ApertureExcitation[BaylissLineSource[FromdB[30], 5, 1], x]

Out[5]=

0.26843876636826486` Sin[π x] + 0.1621540136819705` Sin[3 π x] - 0.00883820909872190 ... ` Sin[5 π x] + 0.002913038090281392` Sin[7 π x] - 0.0007027248993531724` Sin[9 π x]

In[6]:=

Plot[ae, {x, -1/2, 1}] ;

[Graphics:HTMLFiles/index_18.gif]

•BaylissLinearArray

[Graphics:HTMLFiles/index_19.gif]

In[7]:=

AntennaPattern[BaylissLinearArray[FromdB[25], 7, 16, λ/2, λ, θ, φ, α, β]]

Out[7]=

e^(-15/2 i π (-Cos[β] Sin[α] + Cos[φ] Sin[θ])) (-0.1472672554650939` ... 52;])) + 0.1472672554650939` e^(15 i π (-Cos[β] Sin[α] + Cos[φ] Sin[θ])))

In[8]:=

AntennaPattern[BaylissLinearArray[FromdB[25], 7, 16, λ/2, λ, θ]]

Out[8]=

e^(-15/2 i π Sin[θ]) (-0.1472672554650939` - 0.1900317255314121` e^(i π Sin[ ... 0.1900317255314121` e^(14 i π Sin[θ]) + 0.1472672554650939` e^(15 i π Sin[θ]))

Here is the array pattern for a Bayliss linear phased array:

In[9]:=

af = TodB[Abs[AntennaPattern[BaylissLinearArray[FromdB[25], 7, 16, λ/2, λ, θ], ... #952;, 0, π/2}, PlotPoints -> 40, Frame -> True, PlotStyle -> RGBColor[.7, 0, 0]] ;

[Graphics:HTMLFiles/index_25.gif]

Here is the array pattern for the corresponding Bayliss continuoous line source:

In[11]:=

aflinesource = TodB[Abs[AntennaPattern[BaylissLineSource[FromdB[25], 7, 8 λ, λ, _ ... ; afPlotLineSource = Plot[afline, {θ, 0, π/2}, PlotPoints -> 40, Frame -> True] ;

[Graphics:HTMLFiles/index_27.gif]

In[13]:=

Show[afPlotArray, afPlotLineSource] ;

[Graphics:HTMLFiles/index_29.gif]

•BaylissLineB

In[14]:=

UsageMessageCell[BaylissLineB, UsagesOnly -> True]

[Graphics:HTMLFiles/index_31.gif]

Usage message for BaylissLineB

•BaylissLineA

[Graphics:HTMLFiles/index_32.gif]

Usage message for BaylissLineA

•BaylissLineSource

[Graphics:HTMLFiles/index_33.gif]

This is the general analytic expression:

In[15]:=

AntennaPattern[BaylissLineSource[r, nbar, d, λ, θ]]

Out[15]=

((-1)^(-nbar) d (1/λ^2)^(-nbar) (-λ^2)^(-nbar) Gamma[1/2 + nbar]^2 (Underoverscript[ ... ;])/(λ Gamma[1/2 + nbar - (d Sin[θ])/λ] Gamma[1/2 + nbar + (d Sin[θ])/λ])

Numerical results are generated automatically when called for:

In[16]:=

af = TodB[Abs[AntennaPattern[BaylissLineSource[FromdB[25], 7, 8 λ, λ, θ], Normalized -> True]]^2] ; Plot[af, {θ, 0, π/2}, PlotPoints -> 40, Frame -> True] ;

[Graphics:HTMLFiles/index_37.gif]

•BaylissLineU0

[Graphics:HTMLFiles/index_38.gif]

•BaylissLineZ

[Graphics:HTMLFiles/index_39.gif]

Usage message for BaylissLineZ

•BinomialLinearArray

[Graphics:HTMLFiles/index_40.gif]

There is a general expression for the array factor of the binomial array:

In[18]:=

AntennaPattern[BinomialLinearArray[n, d, λ, θ, φ, α, β]]

Out[18]=

e^(i d (1 - n) π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/λ (-e^(2 i d ... ]))/λ + (1 + e^(2 i d π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/λ)^n)

For particular values of n this expands:

In[19]:=

AntennaPattern[BinomialLinearArray[8, λ/2, λ, θ]]

Out[19]=

e^(-7/2 i π Sin[θ]) (-e^(8 i π Sin[θ]) + (1 + e^(i π Sin[θ]))^8)

Here is a normalized version:

In[20]:=

AntennaPattern[BinomialLinearArray[8, λ/2, λ, θ], Normalized -> True]

Out[20]=

1/255 e^(-7/2 i π Sin[θ]) (-e^(8 i π Sin[θ]) + (1 + e^(i π Sin[θ]))^8)

This is an example of a paremetric plot as a functoin of angle of the array pattern (power in dB) normalized to 0 dB at maximum:

In[21]:=

PolarAntennaPlot[AntennaPattern[BinomialLinearArray[8, λ/2, λ, θ], Normalized -> True], {θ, -π, π}, PlotPoints -> 50] ;

[Graphics:HTMLFiles/index_48.gif]

Here is the same but with a different interelement spacing:

In[22]:=

PolarAntennaPlot[AntennaPattern[BinomialLinearArray[8, 3 λ/4, λ, θ], Normalized -> True], {θ, -π, π}, PlotPoints -> 50] ;

[Graphics:HTMLFiles/index_50.gif]

•BinomialLinearArray

[Graphics:HTMLFiles/index_51.gif]

Usage message for BinomialLinearArray

•DolphChebyshevLinearArray

[Graphics:HTMLFiles/index_52.gif]

Usage message for DolphChebyshevLinearArray

•DolphChebyshevLinearArray

[Graphics:HTMLFiles/index_53.gif]

In[23]:=

AntennaPattern[DolphChebyshevLinearArray[r, n, d, λ, θ, φ, α, β], Normalized -> True]

Out[23]=

ChebyshevT[-1 + n, Cos[(d π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/λ] Cosh[ArcCosh[r]/(-1 + n)]]/ChebyshevT[-1 + n, Cosh[ArcCosh[r]/(-1 + n)]]

An 8 element Dolph-Chenyshev array with sidelobes 10 dB below main beam power level:

In[24]:=

PolarAntennaPlot[AntennaPattern[DolphChebyshevLinearArray[FromdB[10/2], 8, λ/2, λ, θ], Normalized -> True], {θ, 0, 2 π}] ;

[Graphics:HTMLFiles/index_57.gif]

Similar to the above but steered -30° off of boresight:

In[25]:=

PolarAntennaPlot[AntennaPattern[DolphChebyshevLinearArray[FromdB[10/2], 8, λ/2, λ, θ, 0, -π/6], Normalized -> True], {θ, 0, 2 π}] ;

[Graphics:HTMLFiles/index_59.gif]

•DolphTschebyscheffLinearArray

[Graphics:HTMLFiles/index_60.gif]

Usage message for DolphTschebyscheffLinearArray

•EffectiveSystemTemperature

[Graphics:HTMLFiles/index_61.gif]

In[26]:=

EffectiveSystemTemperature[t _ a, {t _ 1, t _ 2, t _ 3, t _ 4}, {g _ 1, g _ 2, g _ 3}]

Out[26]=

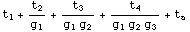
t _ 1 + t _ 2/g _ 1 + t _ 3/(g _ 1 g _ 2) + t _ 4/(g _ 1 g _ 2 g _ 3) + t _ a

•ExplicitPhase

[Graphics:HTMLFiles/index_64.gif]

•GainFactor

[Graphics:HTMLFiles/index_65.gif]

•GaussianBeam

[Graphics:HTMLFiles/index_66.gif]

In[27]:=

AntennaPattern[GaussianBeam[θbw, θ, φ, α, β]]

Out[27]=

2^(-1/2 Csc[θbw]^2 (-Cos[β] Sin[α] + Cos[φ] Sin[θ])^2)

In[28]:=

AntennaPattern[GaussianBeam[θbw, θ]]

Out[28]=

2^(-1/2 Csc[θbw]^2 Sin[θ]^2)

In[29]:=

AntennaPattern[GaussianBeam[θbw, θ, ExplicitPhase -> Exp[I γ], GainFactor -> g]]

Out[29]=

2^(-1/2 Csc[θbw]^2 Sin[θ]^2) e^(i γ) g

In[30]:=

PolarAntennaPlot[AntennaPattern[GaussianBeam[π/20, θ]], {θ, -π, π}] ;

[Graphics:HTMLFiles/index_74.gif]

•GeneralLinearArray

[Graphics:HTMLFiles/index_75.gif]

With the choice of function as simply unity ( expressed as a pure function by 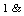1 & we get the uniform array that is examined below under UniformLinearArray:

In[31]:=

glaAntennaPattern = AntennaPattern[GeneralLinearArray[1 &, n, d, λ, θ, 0, 0, 0]]

Out[31]=

(e^(i d (1 - n) π Sin[θ])/λ (-1 + e^(2 i d n π Sin[θ])/λ))/(-1 + e^(2 i d π Sin[θ])/λ)

Bringing this into a (perhaps) more familiar form:

In[32]:=

FullSimplify[ExpToTrig[glaAntennaPattern]]

Out[32]=

Csc[(d π Sin[θ])/λ] Sin[(d n π Sin[θ])/λ]

The first argument of GeneralLinearArray can also be a list of array weights.  This corresponds to an array with 5 equally weighted elements:

In[33]:=

uniform5 = AntennaPattern[GeneralLinearArray[Table[1, {5}], 5, d, λ, θ]]

Out[33]=

1 + e^(-(2 i d π Sin[θ])/λ) + e^(2 i d π Sin[θ])/λ + e^(-(4 i d π Sin[θ])/λ) + e^(4 i d π Sin[θ])/λ

In[34]:=

FullSimplify[uniform5 - glaAntennaPattern /. n -> 5]

Out[34]=

0

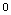
Here is the array factor for weights that vary according to the form (give as a pure function) Cos[(π #)/n] &:

In[35]:=

AntennaPattern[GeneralLinearArray[Cos[(π #)/n] &, n, d, λ, θ, 0, 0, 0]]

Out[35]=

(i e^((i d (3 - n) π Sin[θ])/λ + (2 i d n π Sin[θ])/λ) (-1 + e^( ... e^(2 i d π Sin[θ])/λ) (-1 + e^((i π)/n + (2 i d π Sin[θ])/λ)))

Here is its normalized form for n=6 with an inter element spacing d=λ/2 steered to an angle of 45 degrees:

In[36]:=

cosAntennaPattern6 = AntennaPattern[GeneralLinearArray[Cos[(π #)/6] &, 6, λ/2, λ, θ, 0, π/4, 0], Normalized -> True]

Out[36]=

((7 - 4 3^(1/2))^(1/2) e^(-3/2 i π (-1/2^(1/2) + Sin[θ])) (1 + e^(6 i π (-1/2^( ... - 2 3^(1/2) e^(i π (-1/2^(1/2) + Sin[θ])) + 2 e^(2 i π (-1/2^(1/2) + Sin[θ])))

In[37]:=

PolarAntennaPlot[cosAntennaPattern6, {θ, -π, π}] ;

[Graphics:HTMLFiles/index_91.gif]

As another example we consider an asymmetric distribution of array weights (this will lead to a monopulse type beam pattern):

In[38]:=

Clear[assymetricTriangle] ; assymetricTriangle[n_] := If[# >= 0, 1 - #/n, -#/n - 1] &

In[40]:=

Plot[assymetricTriangle[5][x], {x, -5, 5}] ;

[Graphics:HTMLFiles/index_94.gif]

Here is an example for a 6-element 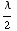λ/2 array:

In[41]:=

numberOfArrayElements = 6 ;

In[42]:=

AntennaPattern[GeneralLinearArray[assymetricTriangle[numberOfArrayElements], numberOfArrayElements, λ/2, λ, θ, 0, π/4, 0]]

Out[42]=

1/6 e^(-5/2 i π (-1/2^(1/2) + Sin[θ])) (-3 - 4 e^(i π (-1/2^(1/2) + Sin[θ] ... 2;])) + 5 e^(4 i π (-1/2^(1/2) + Sin[θ])) + 4 e^(5 i π (-1/2^(1/2) + Sin[θ])))

Since this array will have a two-lobed (monopulse) main beam, we need to determine the location of a maximum to normalize.  To do this we use a function from the Mathematica standard add-on package NumericalMath`NMinimize`,  NMaximize.

First load the package:

In[43]:=

Needs["NumericalMath`NMinimize`"]

In[44]:=

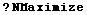
? NMaximize

NMaximize[{obj, cons}, vars] searches for a global maximum of the function obj subject to the constraints cons, with variables vars.

NMaximize[{obj, cons}, vars] searches for a global maximum of the function obj subject to the constraints cons, with variables vars.

Now find the position of a maximum for a 10 element array:

In[45]:=

NMaximize[{Abs[AntennaPattern[GeneralLinearArray[assymetrictriangle[10], 10, 1/2, 1, θ, 0, 0, 0], Normalized -> True]]}, θ]

Out[45]=

NMaximize[{Abs[AntennaPattern[GeneralLinearArray[assymetrictriangle[10], 10, 1/2, 1, θ, 0, 0, 0], Normalized -> True]]}, θ]

This also shows us that the angle between the two monopulse beams is (in degrees):

In[46]:=

2 (0.160008 180/π)

Out[46]=

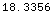
18.335566176658556`

The slope of the pattern on boresight is also easily determined via similar methods.

Finally plot the normalized result:

In[47]:=

PolarAntennaPlot[AntennaPattern[GeneralLinearArray[assymetrictriangle[10], 10, λ/2, λ ... 797807027956, 0, 0, 0}], Normalized -> True], {θ, -π, π}, PlotPoints -> 50] ;

[Graphics:HTMLFiles/index_108.gif]

The monopulse pattern in this broadside configuration is clear.

•NormalizationPoint

[Graphics:HTMLFiles/index_109.gif]

In[48]:=

PackagesAndFunctionsWithOption[NormalizationPoint]

Out[48]//DisplayForm=

[Graphics:HTMLFiles/index_111.gif]

•Normalized

[Graphics:HTMLFiles/index_112.gif]

In[49]:=

PackagesAndFunctionsWithOption[Normalized]

Out[49]//DisplayForm=

[Graphics:HTMLFiles/index_114.gif]

•Overhang

[Graphics:HTMLFiles/index_115.gif]

In[50]:=

PackagesAndFunctionsWithOption[Overhang]

Out[50]//DisplayForm=

[Graphics:HTMLFiles/index_117.gif]

•TaylorLinearArray

[Graphics:HTMLFiles/index_118.gif]

In[51]:=

AntennaPattern[TaylorLinearArray[FromdB[25], 2, 3, λ/2, λ, θ, φ, α, β]]

Out[51]=

(e^(-i π (-Cos[β] Sin[α] + Cos[φ] Sin[θ])) ((4 - e^(i π (-Cos[&# ... 52;]))) ArcCosh[(5 Log[100000])/Log[10]]^2))/(4 (π^2 + 4 ArcCosh[(5 Log[100000])/Log[10]]^2))

In[52]:=

AntennaPattern[TaylorLinearArray[FromdB[25], 2, 3, λ/2, λ, θ]]

Out[52]=

(e^(-i π Sin[θ]) ((4 - e^(i π Sin[θ]) + 4 e^(2 i π Sin[θ])) ` ... 952;])) ArcCosh[(5 Log[100000])/Log[10]]^2))/(4 (π^2 + 4 ArcCosh[(5 Log[100000])/Log[10]]^2))

In[53]:=

AntennaPattern[TaylorLinearArray[FromdB[25], 2, 3, λ/2, λ, θ, Overhang -> 2 λ]]

Out[53]=

(e^(-i π Sin[θ]) ((11 - 5 5^(1/2) - 4 e^(i π Sin[θ]) + (11 - 5 5^(1/2)) e^ ... 52;])) ArcCosh[(5 Log[100000])/Log[10]]^2))/(16 (π^2 + 4 ArcCosh[(5 Log[100000])/Log[10]]^2))

To avoid generating very large exact expressions we use floating point values for the calculation:

In[54]:=

AntennaPattern[TaylorLinearArray[NFromdB[25], 7, 16, λ/2, λ, θ, φ, α, β]]

Out[54]=

e^(-15/2 i π (-Cos[β] Sin[α] + Cos[φ] Sin[θ])) (0.5104308569740004` ... 52;])) + 0.5104308569740004` e^(15 i π (-Cos[β] Sin[α] + Cos[φ] Sin[θ])))

In[55]:=

AntennaPattern[TaylorLinearArray[NFromdB[25], 7, 16, λ/2, λ, θ]]

Out[55]=

e^(-15/2 i π Sin[θ]) (0.5104308569740004` + 0.5871267773950055` e^(i π Sin[ ... 0.5871267773950055` e^(14 i π Sin[θ]) + 0.5104308569740004` e^(15 i π Sin[θ]))

In[56]:=

afarray = TodB[Abs[AntennaPattern[TaylorLinearArray[NFromdB[40], 2, 16, λ/2, λ, _ ... #952;, 0, π/2}, PlotPoints -> 40, Frame -> True, PlotStyle -> RGBColor[.7, 0, 0]] ;

[Graphics:HTMLFiles/index_130.gif]

In[58]:=

aflinesource = TodB[Abs[AntennaPattern[TaylorLineSource[FromdB[40], 2, 8 λ, λ, θ ... otLineSource = Plot[aflinesource, {θ, 0, π/2}, PlotPoints -> 40, Frame -> True] ;

[Graphics:HTMLFiles/index_132.gif]

In[60]:=

Show[afPlotArray, afPlotLineSource] ;

[Graphics:HTMLFiles/index_134.gif]

In[61]:=

AntennaPattern[TaylorLinearArray[r, nbar, 4, d, λ, θ]]

Out[61]=

e^(-(3 i d π Sin[θ])/λ) (1 + e^(2 i d π Sin[θ])/λ + e^(4 i d ... citationCoeff[r, nbar, K] Cos[(2 π (3 d + 1/2 (-3 d - λ) + λ/2) K)/(3 d + λ)])

•TaylorLineA

[Graphics:HTMLFiles/index_137.gif]

Usage message for TaylorLineA

•TaylorLineExcitationCoeff

[Graphics:HTMLFiles/index_138.gif]

Usage message for TaylorLineExcitationCoeff

•TaylorLineSource

[Graphics:HTMLFiles/index_139.gif]

In[62]:=

AntennaPattern[TaylorLineSource[r, nbar, L, λ, θ]]

Out[62]=

(λ Csc[θ] (-1 + nbar) !^2 (Underoverscript[∏, K = 1, arg3] (1 - (L^2 Sin[θ ... chhammer[1 - (L Sin[θ])/λ, -1 + nbar] Pochhammer[1 + (L Sin[θ])/λ, -1 + nbar])

In[63]:=

AntennaPattern[TaylorLineSource[r, 3, L, λ, θ]]

Out[63]=

(4 λ Csc[θ] (1 - (L^2 (25/4 + ArcCosh[(10 Log[r])/Log[10]]^2/π^2) Sin[θ]^2 ... ])/λ) (2 - (L Sin[θ])/λ) (1 + (L Sin[θ])/λ) (2 + (L Sin[θ])/λ))

In[64]:=

PowerExpand[ApertureExcitation[TaylorLineSource[FromdB[rdb], 3, L, λ], x]]

Out[64]=

1 + 2 (2/3 (1 - (25/4 + ArcCosh[rdb]^2/π^2)/(9 (1/4 + ArcCosh[rdb]^2/π^2))) (1 - (25 ... 1 - (4 (25/4 + ArcCosh[rdb]^2/π^2))/(9 (9/4 + ArcCosh[rdb]^2/π^2))) Cos[(4 π x)/L])

•TaylorLineZ

[Graphics:HTMLFiles/index_146.gif]

Usage message for TaylorLineZ

•TryZTransform

[Graphics:HTMLFiles/index_147.gif]

Usage message for TryZTransform

•UniformLinearArray

[Graphics:HTMLFiles/index_148.gif]

In[65]:=

AntennaPattern[UniformLinearArray[n, d, λ, θ, φ, α, β]]

Out[65]=

Csc[(d π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/λ] Sin[(d n π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/λ]

In[66]:=

AntennaPattern[UniformLinearArray[n, d, λ, θ, 0, α, 0]]

Out[66]=

Csc[(d π (-Sin[α] + Sin[θ]))/λ] Sin[(d n π (-Sin[α] + Sin[θ]))/λ]

In[67]:=

AntennaPattern[UniformLinearArray[n, d, λ, θ, 0, α, 0], Normalized -> True]

Out[67]=

(Csc[(d π (-Sin[α] + Sin[θ]))/λ] Sin[(d n π (-Sin[α] + Sin[θ]))/λ])/n

In terms of the frequency f:

In[68]:=

AntennaPattern[UniformLinearArray[n, d, Wavelength[f], θ, φ, α, β]]

Out[68]=

Csc[(d f π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/299792458] Sin[(d f n π (-Cos[β] Sin[α] + Cos[φ] Sin[θ]))/299792458]

For steering angles α, β=0 and an elment spacing of 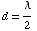d = λ/2:

In[69]:=

AntennaPattern[UniformLinearArray[n, λ/2, λ, θ], Normalized -> True]

Out[69]=

(Csc[1/2 π Sin[θ]] Sin[1/2 n π Sin[θ]])/n

In[70]:=

Plot[AntennaPattern[UniformLinearArray[12, λ/2, λ, θ], Normalized -> True], {θ, -π/2, π/2}, Frame -> True, PlotRange -> All] ;

[Graphics:HTMLFiles/index_161.gif]

In[71]:=

Plot[TodB[Abs[AntennaPattern[UniformLinearArray[15, λ/2, λ, θ], Normalized -> True]]], {θ, -π/2, π/2}, Frame -> True] ;

[Graphics:HTMLFiles/index_163.gif]

Broadside:

In[72]:=

PolarPlot[Abs[AntennaPattern[UniformLinearArray[6, λ/2, λ, θ], Normalized -> ... -1, 1}}, PlotStyle -> {AbsoluteThickness[2], Hue[.7]}, Frame -> True, ImageSize -> 300] ;

[Graphics:HTMLFiles/index_165.gif]

Steered to a phase 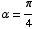α = π/4:

In[73]:=

PolarPlot[Abs[AntennaPattern[UniformLinearArray[6, λ/2, λ, θ, 0, π/4], Nor ... -1, 1}}, PlotStyle -> {AbsoluteThickness[2], Hue[.7]}, Frame -> True, ImageSize -> 300] ;

[Graphics:HTMLFiles/index_168.gif]

In[74]:=

PolarAntennaPlot[AntennaPattern[UniformLinearArray[6, λ/2, λ, θ, 0, π/6], Normalized -> True], {θ, -π, π}] ;

[Graphics:HTMLFiles/index_170.gif]

Compare broadside with endfire:

In[75]:=

PolarAntennaPlot[{AntennaPattern[UniformLinearArray[6, λ/2, λ, θ], Normalized - ... s -> 30, PlotStyle -> {{AbsoluteThickness[2], Hue[.9]}, {AbsoluteThickness[2], Hue[.66]}}] ;

[Graphics:HTMLFiles/index_172.gif]

For further information on our services send email to info@scientificarts.com .
Contents of this web site Copyright © 1999-2011, Scientific Arts, LLC.

d